SamplePublisher`GrassmannCalculus`
TrigonometricSubstitution |
|
| | ||||
Details and Options
Examples
(1)
Basic Examples
(1)
In[1]:=
<<GrassmannCalculus`
Define 1-dimensional x and θ spaces.
In[2]:=
xSpace:=SetEuclideanNSpace[1,{x},"Form"];θSpace:=SetEuclideanNSpace[1,{θ},"Form"];
In[3]:=
xSpace;Print["Original integral:"]xIntegral=
Undefined,dxPrint"Perform the trigonometric substitution ",x
{xSpace,θSpace,subRules},x
FormIntegral |
6
x
25-1
2
x
1/25
Sec[θ]," with display of the associated triangle"θIntegral1=xIntegral//TrigonometricSubstitution |
1/25
Sec[θ]Print["Substitute for absolute value:"]θIntegral=θIntegral1/.Abs[Tan[θ]]2
Tan[θ]
Original integral:
Out[3]=
∫
ℴ
6dx
x
-1+25
2
x
Perform the trigonometric substitution x with display of the associated triangle
Sec[θ]
5
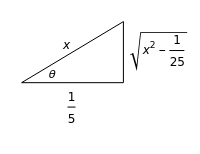
Out[3]=
∫
ℴ
Substitute for absolute value:
Out[3]=
∫
ℴ
2
Tan[θ]
The subRules Association is:
In[4]:=
subRules
Out[4]=
TanTan[θ]5,SinSin[θ],CscCsc[θ],CosCos[θ],SecSec[θ]5x,angleθArcSec[5x],domain0≤θ<&&5x≥1||<θ≤π&&5x≤-1
-+
,CotCot[θ]1
25
2
x
1
5
-+
1
25
2
x
-+
1
25
2
x
x
x
-+
1
25
2
x
1
5x
π
2
π
2
The domain and angle substitution for the trigonometric substitution are extracted by:
In[5]:=
subRules["domain"]subRules["angle"]
Out[5]=
0≤θ<&&5x≥1||<θ≤π&&5x≤-1
π
2
π
2
Out[5]=
θArcSec[5x]
Switch to θ space, evaluate the integral, reverse substitute and simplify for the domain.
In[6]:=
θSpace;step1=
[θIntegral]step2=step1/.subRules["angle"]FullSimplify[step2,subRules["domain"]]
EvaluateFormIntegrals |
Out[6]=
6θCot[θ]
2
Tan[θ]
Out[6]=
6
1-
ArcSec[5x]1
25
2
x
2
x
1-
x1
25
2
x
Out[6]=
6ArcSec[5x]Sign[x]
|
|
""

