SamplePublisher`GrassmannCalculus`
EvaluateFormIntegrals |
|
| | ||||
Details and Options
Examples
(15)
Basic Examples
(1)
In[1]:=
<<GrassmannCalculus`
To find the area between two curves;
In[2]:=
SetCoordinateVectorSpace |
FormIntegral |
EvaluateFormIntegrals |
Out[2]=
∫
ℴ
Out[2]=
2
2
The following form of the integral, using domain iterators, is more easily evaluated. Show the unevaluated Mathematica Integrate statement.
In[3]:=
domain={{x,π/4,5π/4},{y,Cos[x],Sin[x]}};
[domain,dx⋀dy]
[%,InactiveIntegralTrue]Activate[%]
FormIntegral |
EvaluateFormIntegrals |
Out[3]=
∫
ℴ
Out[3]=
5π
4
∫
π
4
Sin[x]
∫
Cos[x]
Out[3]=
2
2
Evaluate an integral that uses a Region and a parameter. Without an Assumptions option we obtain a . We also show the unevaluated statement generated.
ConditionalExpression
Integrate
In[4]:=
FormIntegral |
EvaluateFormIntegrals |
Out[4]=
∫
ℴ
Out[4]=
ConditionalExpression[π,R>0]
2
R
In the following we add an Assumption.
In[5]:=
FormIntegral |
EvaluateFormIntegrals |
Out[5]=
∫
ℴ
Out[5]=
π
2
R
The following uses a .
ParametricRegion
In[6]:=
SetCoordinateVectorSpace |
2
x
FormIntegral |
EvaluateFormIntegrals |
Out[6]=
ParametricRegion[{{x,-y+(1+y)},-1≤x≤1&&0≤y≤1},{x,y}]
2
x
Out[6]=
∫
ℴ
Out[6]=
4
3
The following integrates a Gaussian over a full 1-dimensional space.
In[7]:=
SetCoordinateVectorSpace |
FormIntegral |
2
x
EvaluateFormIntegrals |
Out[7]=
∫
ℴ
-
2
x
2
Out[7]=
2π
The following integrates over a discretized disk.
In[8]:=
SetCoordinateVectorSpace |
FormIntegral |
EvaluateFormIntegrals |
Out[8]=
∫
ℴ
Out[8]=
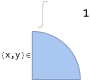
Out[8]=
0.785398
In this case, it did not have to be discretized.
In[9]:=
SetCoordinateVectorSpace |
FormIntegral |
EvaluateFormIntegrals |
Out[9]=
∫
ℴ
Out[9]=
π
4
In[10]:=
SetCoordinateVectorSpace |
FormIntegral |
EvaluateFormIntegrals |
Out[10]=
ParametricRegion[{{x,Sin[x]},0≤x≤π},{x}]
Out[10]=
∫
ℴ
Out[10]=
2
2
EllipticE1
2
Here is a line integral using a . We need a 2-dimensional space even though it's a 1-dimensional integral.
ParametricRegion
In[11]:=
SetCoordinateVectorSpace |
FormIntegral |
EvaluateFormIntegrals |
Out[11]=
∫
ℴ
Out[11]=
2
2
EllipticE1
2
Out[11]=
3.8202
The following is a Gaussian integrated over a square centered at the origin.
In[12]:=
SetCoordinateVectorSpace |
FormIntegral |
2
x
2
y
EvaluateFormIntegrals |