SamplePublisher`GrassmannCalculus`
ContractorRules |
|
| | ||||
Details and Options
Examples
(1)
Basic Examples
(1)
In[1]:=
<<GrassmannCalculus`
In[2]:=
SetCoordinateVectorSpace |
The rules for evaluating scalar Contractors are:
In[3]:=
ContractorRules |
Out[3]=
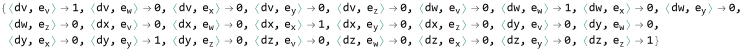
The basis vectors can be obtained by:
In[4]:=
Drop
,1Drop
,1
VectorBasis |
FormBasis |
Out[4]=
{,,,,}
e
v
e
w
e
x
e
y
e
z
Out[4]=
{dv,dw,dx,dy,dz}
The basis elements are also available on the Grassmann Symbols palette from the Palettes menu, or obtained by.
In[5]:=
GrassmannSymbolsPalette |
ContractorRules
In[6]:=
Outer
,1,Drop
,1//MatrixForm%/.
[]//MatrixForm
#1,#2
&,DropFormBasis |
VectorBasis |
ContractorRules |
Out[6]//MatrixForm=

Out[6]//MatrixForm=
1 | 0 | 0 | 0 | 0 |
0 | 1 | 0 | 0 | 0 |
0 | 0 | 1 | 0 | 0 |
0 | 0 | 0 | 1 | 0 |
0 | 0 | 0 | 0 | 1 |
ContractorRules[] can only be used on scalar Contractors. As an example:
In[7]:=
〈
adx+bdy,ce
x
e
y
〉
%//GrassmannBreakout |
Contractor |
ContractorRules |
Out[7]=
〈adx+bdy,c+d〉
e
x
e
y
Out[7]=
ac〈dx,〉+ad〈dx,〉+bc〈dy,〉+bd〈dy,〉
e
x
e
y
e
x
e
y
Out[7]=
ac+bd
Higher order Contractors must be reduced to scalar Contractors with , which then automatically evaluates them.
In[8]:=
〈
dv⋀dw⋀dx⋀dy,e
w
e
y
〉
%//ToScalarContractors |
Out[8]=
〈dv⋀dw⋀dx⋀dy,⋀〉
e
w
e
y
Out[8]=
-(dv⋀dx)
|
""

