GrassmannCalculus`
GradeComplement  |
|
| | ||||
Details and Options
Examples
(1)
Basic Examples
(1)
In[1]:=
<<GrassmannCalculus`
In the algebra of 3-space with default basis, the basis of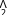 
is:
In[2]:=
★A;
[2]
 | GradeBasis |
Out[2]=
{⋀,⋀,⋀}
e
1
e
2
e
1
e
3
e
2
e
3
With a Euclidean metric, the complements of these basis elements are:
In[3]:=
 | GradeComplement |
Out[3]=
{,-,}
e
3
e
2
e
1
However, with a general metric, the complements of the basis elements of 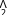are a little more complex.
In[4]:=
| DeclareMetric |
| GradeComplement |
Out[4]=
-++(-)+(-+),(-+)+-+(-+),(-+)+(-)+-+
e
3
2
g
1,2
g
1,1
g
2,2
★g
e
2
g
1,2
g
1,3
g
1,1
g
2,3
★g
e
1
g
1,3
g
2,2
g
1,2
g
2,3
★g
e
3
g
1,2
g
1,3
g
1,1
g
2,3
★g
e
2
2
g
1,3
g
1,1
g
3,3
★g
e
1
g
1,3
g
2,3
g
1,2
g
3,3
★g
e
3
g
1,3
g
2,2
g
1,2
g
2,3
★g
e
2
g
1,3
g
2,3
g
1,2
g
3,3
★g
e
1
2
g
2,3
g
2,2
g
3,3
★g
Here, the symbol denotes the determinant of the metric tensor. You can obtain its value explicitly in terms of the components of the currently declared metric tensor by using . For Example:
★g
ToMetricElements
In[5]:=
| ★g |
| ToMetricElements |
Out[5]=
-+2-+-+
2
g
1,3
g
2,2
g
1,2
g
1,3
g
2,3
2
g
1,2
g
3,3
g
1,1
2
g
2,3
g
2,2
g
3,3
This can also be obtained directly by , which is calculated whenever a new metric is declared.
GrassmannVolumeFactor
In[6]:=
GrassmannVolumeFactor
Out[6]=
-+2-+-+
2
g
1,3
g
2,2
g
1,2
g
1,3
g
2,3
2
g
1,2
g
3,3
g
1,1
2
g
2,3
g
2,2
g
3,3
 |
|
 |
|
""