In[]:=
(*deployswithcanonicalname*)deploy""
Wed 27 Mar 2024 16:20:16
Free probability
parent doc: Free Probability section
Log:
- Mar 27: diagrams for AAAA’A’A’ question
- Mar 25: wicks visualization: question
- Feb 19: disentangling question on math.SE with Robert Israel answer, cleaned-up forum-disentangling.nb
- Feb 18: Mathematica formulas question of Ben’s code mathematica.SE, getting formulas like+10+4n
- Dec 4: stats.SE Sangchul update, also math.SE Ben update on Mathematica code to compute arbitrary formulas
- Dec 3: mathoverflow expression for trace of product,
- Dec 2: forum-gaussian-second-moment.nb, update Disentanging results
- Dec 1:+n formula from Sangchul Lee about counting cycles, math.SE “Showing ” post
- Nov 25: math.SE q on product of matrices X1 X2 X3 with inductive proof
- Nov 24: simulation results colab
- Nov 24: forum-random-matrix-moments.nb
- Nov 24: stats.SE q on product of matrices X1 X2 X3 with inductive proof on E[XCX’] from amoeba
- Oct: forked from NN<>LeastSquares-2.nb
- July 19: mathematica.SE “Obtaining asymptotics of parametrically defined function” post
Mathematica:
- purity-of-matrix-products.nb (Mathoverflow post, my own answer)
- Frobenius norm of product of random matrices
- sent to Thomas thomas-convergence-of-rank.nb
- forum-burda-evals.nb (checking for commutativity)
- forum-product-of-matrices.nb
- formula-check.nb
Notability:
- Formulas-contents notability (”dot product formulas”)
- “NN<>Least Squares” notability (Frobenius/Trace/Rank)
Posts:
- Nov 24: math.SE and stats.SE “Frobenius norm of a product of Gaussian matrices” math.SE post, stats.SE post
- Sep 11 “Estimating the sum of 4th powers of singular values?” scicomp post (notebook)
Log:
- Mar 27: diagrams for AAAA’A’A’ question
- Mar 25: wicks visualization: question
- Feb 19: disentangling question on math.SE with Robert Israel answer, cleaned-up forum-disentangling.nb
- Feb 18: Mathematica formulas question of Ben’s code mathematica.SE, getting formulas like
4
n
2
n
- Dec 4: stats.SE Sangchul update, also math.SE Ben update on Mathematica code to compute arbitrary formulas
- Dec 3: mathoverflow
3
n
- Dec 2: forum-gaussian-second-moment.nb, update Disentanging results
- Dec 1:
3
n
ETr(AA)+2n
T
A
T
A
3
n
- Nov 25: math.SE q on product of matrices X1 X2 X3 with inductive proof
- Nov 24: simulation results colab
- Nov 24: forum-random-matrix-moments.nb
- Nov 24: stats.SE q on product of matrices X1 X2 X3 with inductive proof on E[XCX’] from amoeba
- Oct: forked from NN<>LeastSquares-2.nb
- July 19: mathematica.SE “Obtaining asymptotics of parametrically defined function” post
Mathematica:
- purity-of-matrix-products.nb (Mathoverflow post, my own answer)
- Frobenius norm of product of random matrices
- sent to Thomas thomas-convergence-of-rank.nb
- forum-burda-evals.nb (checking for commutativity)
- forum-product-of-matrices.nb
- formula-check.nb
Notability:
- Formulas-contents notability (”dot product formulas”)
- “NN<>Least Squares” notability (Frobenius/Trace/Rank)
Posts:
- Nov 24: math.SE and stats.SE “Frobenius norm of a product of Gaussian matrices” math.SE post, stats.SE post
- Sep 11 “Estimating the sum of 4th powers of singular values?” scicomp post (notebook)
Burda, Eigenvalues of Powers of Gaussian (nMarchenko law)
Burda, Eigenvalues of Powers of Gaussian law)
(
n
Marchenko
3.59-3.60 of https://arxiv.org/pdf/1510.06128.pdf
Also https://iopscience.iop.org/article/10.1088/1742-6596/473/1/012002/pdf
forum-burda-evals.nb
Also https://iopscience.iop.org/article/10.1088/1742-6596/473/1/012002/pdf
forum-burda-evals.nb
In[]:=
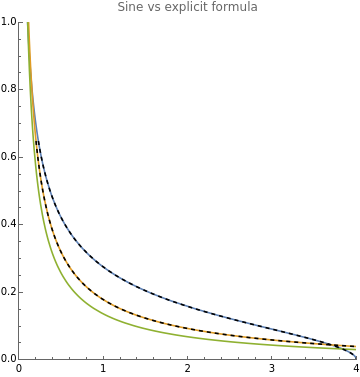
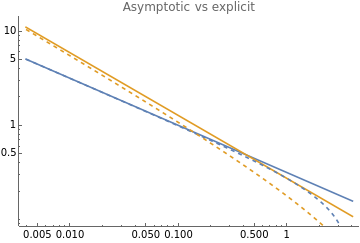
Clear[x];pdf=-6;ClearAll["Global`*"];Clear[x];x[t_]:=;y[t_]:=;clip[a_]:=Clipa,0,;nvals=Range[3];sf={"Log","Log"};SF=StringForm;legends=SF["n=``",#]&/@nvals;funcs=Table[{x@clip@t,y@clip@t},{n,nvals}];parametric=ParametricPlot@@{funcs,{t,0,Pi},PlotRange->{{0,4},{0,1}},AspectRatio->1,PlotLabel->"Sine vs explicit formula",PlotLegends->legends};pdf2=-6;marchenko=PDF[MarchenkoPasturDistribution[1],x];(*cdf2=Assuming[{0<x<1/100},Integrate[pdf2,{x,0,y}]]/.y->x*)explicit=Plot[{marchenko,pdf2},{x,0,4},PlotStyle->{{Black,Bold,Dashed},{Black,Bold,Dashed}},PlotLegends->{"Marchenko Pastur","Burda"}];Show[parametric,explicit]explicit=Plot[{marchenko,pdf2},{x,0,4},PlotStyle->{{Bold,Dashed},{Bold,Dashed}},PlotLegends->{"Marchenko Pastur","Burda"},ScalingFunctions->sf];approx=Plot@@TableSin,{n,{1,2}},{x,0,4},ScalingFunctions->sf,PlotLabel->"Asymptotic vs explicit";Show[approx,explicit]n=2;Clear[x];makeFoxH[n_]:=(top={{0,1},{2-n,n}};topleft={};topright={{0,1},{1,1}};bottom={{-1,2}};bottomleft={{-n,n+1}};bottomright={};specs={{topleft,topright},{bottomleft,bottomright}};FoxH[{topleft,topright},{bottomleft,bottomright},x]);explicit=Plot[{marchenko,pdf2},{x,0,4},PlotStyle->{{Bold,Dashed},{Bold,Dashed}},PlotLegends->{"Marchenko Pastur","Burda"},ScalingFunctions->sf];fox=Plot@@{makeFoxH/@{1,2},{x,0,1},ScalingFunctions->sf};Show[explicit,fox,PlotLabel->"FoxH vs explicit"]
1/3
2
1/2
3
12Pi
1/3
2
2/3
27+
27(27-4x)
1/3
x
2/3
x
1/3
27+
27(27-4x)
n+1
Sin[(n+1)t]
Sin[t]
n
Sin[nt]
2
Sin[t]
n-1
Sin[nt]
π
n
Sin[(n+1)t]
Pi
n+1
1/3
2
1/2
3
12Pi
1/3
2
2/3
27+
27(27-4x)
1/3
x
2/3
x
1/3
27+
27(27-4x)
-1+
1
1+n
x
π
1+n
π
Out[]=
Out[]=
Out[]=
Construct MeijerG:
1/n
1/n
In[]:=
Solve-6==0,x
1/3
2
1/2
3
12Pi
1/3
2
2/3
27+
27(27-4x)
1/3
x
2/3
x
1/3
27+
27(27-4x)
Out[]=
x
27
4
Moments of Fuchs-Catalan density
Moments of Fuchs-Catalan density
Ipsen, J. R. 2015. “Products of Independent Gaussian Random Matrices.” arXiv [math-Ph]. arXiv. http://arxiv.org/abs/1510.06128.
Formula 3.59
Formula 3.59
Gaussian matrix moments
Gaussian matrix moments
Solve using S-transform
Solve using S-transform
Now for squared Wishart
Simplified solving using S-transform
Simplified solving using S-transform
Least squares on Gaussian random data
Least squares on Gaussian random data
Density after many matrix products
Density after many matrix products
Main doc: https://www.wolframcloud.com/obj/yaroslavvb/nn-linear/forum-product-of-matrices.nb
Mo question: https://mathoverflow.net/questions/451732/what-does-a-product-of-many-gaussian-matrices-converge-to
Mo question: https://mathoverflow.net/questions/451732/what-does-a-product-of-many-gaussian-matrices-converge-to
Convergence of effective rank
Convergence of effective rank
Isometry/Ahle
Isometry/Ahle
TLDR; information is kept on isometries, but isometry + small noise will lose it