In[]:=
(*deployswithcanonicalname*)deploy
Sat 25 Nov 2023 12:04:18
Burda vs Ipsen formulas
Burda vs Ipsen formulas
In[]:=
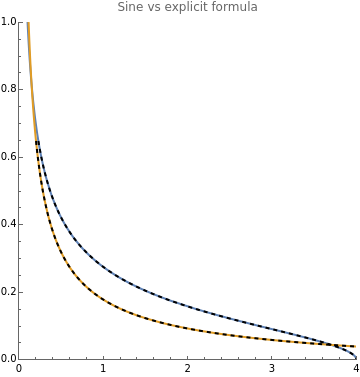
ClearAll["Global`*"];Clear[x];x[t_]:=;y[t_]:=;clip[a_]:=Clipa,0,;nvals=Range[2];sf={"Log","Log"};SF=StringForm;legends=SF["Ipsen n=``",#]&/@nvals;funcs=Table[{x@clip@t,y@clip@t},{n,nvals}];parametric=ParametricPlot@@{funcs,{t,0,Pi},PlotRange->{{0,4},{0,1}},AspectRatio->1,PlotLabel->"Sine vs explicit formula",PlotLegends->legends};pdf2=-6;marchenko=PDF[MarchenkoPasturDistribution[1],x];(*cdf2=Assuming[{0<x<1/100},Integrate[pdf2,{x,0,y}]]/.y->x*)explicit=Plot[{marchenko,pdf2},{x,0,4},PlotStyle->{{Black,Bold,Dashed},{Black,Bold,Dashed}},PlotLegends->{"Marchenko Pastur","Burda"}];Show[parametric,explicit]
n+1
Sin[(n+1)t]
Sin[t]
n
Sin[nt]
2
Sin[t]
n-1
Sin[nt]
π
n
Sin[(n+1)t]
Pi
n+1
1/3
2
1/2
3
12Pi
1/3
2
2/3
27+
27(27-4x)
1/3
x
2/3
x
1/3
27+
27(27-4x)
Out[]=
Spectral commutativity example
Spectral commutativity example
In[]:=
evalsBurda[X_,Y_]:=Eigenvalues[X.X.Y.Y];evalsMine[X_,Y_]:=Eigenvalues[(X.X.Y.Y)];SeedRandom[1];getVal[n_]:={X,Y}=RandomVariate[NormalDistribution[],{2,n,n}];;nvals={10,100,1000};TableForm[{nvals,getVal/@nvals},TableHeadings->{{"d","discrepancy"}}]
Norm[evalsBurda[X,Y]-evalsMine[X,Y]]
Min[Norm@evalsBurda[X,Y],Norm@evalsMine[X,Y]]
Out[]//TableForm=
d | 10 | 100 | 1000 |
discrepancy | 0.443187 | 0.055588 | 0.0088276 |