In[]:=
Fri 6 Oct 2023 12:35:33
forked from https://www.wolframcloud.com/obj/yaroslavvb/nn-linear/NN%3C%3ELeastSquares-2.nb
Convergence of effective rank
Convergence of effective rank
- Formulas-contents: dot product formulas: notability
- formula-check.nb
- purity-of-matrix-products.nb
- scicomp (Effective algorithm): https://scicomp.stackexchange.com/questions/43039/estimating-the-sum-of-4th-powers-of-singular-values/43044#43044
- formula-check.nb
- purity-of-matrix-products.nb
- scicomp (Effective algorithm): https://scicomp.stackexchange.com/questions/43039/estimating-the-sum-of-4th-powers-of-singular-values/43044#43044
1. fast effective rank https://www.wolframcloud.com/obj/yaroslavvb/nn-linear/forum-sum-of-singular-vals.nb
2. reply scicomp done
3. mo plots
2. reply scicomp done
3. mo plots
Out[]=
In[]:=
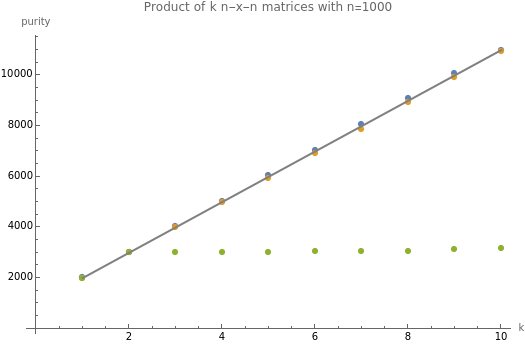
normal=NormalDistribution[];uniform=UniformDistribution[{-1,1}];dist=normal;matsNormal=NestList[#.sample&,sample,maxK-1];dist=uniform;matsUniform=NestList[#.sample&,sample,maxK-1];(*Productofkrandommatrices*)randomProduct[k_]:=Nest[#.sample&,sample,k-1];center[mat_]:=(mat-Mean[Flatten@mat]);relu[mat_]:=Clip[mat,{0,∞}];matsRelu=NestList[center@Abs@#.sample&,sample,maxK-1];observedPlot=ListPlot[(npurity2/@#)&/@{matsNormal,matsUniform,matsRelu},PlotLegends->{"Normal entries","Uniform entries","Normal+clip+center"}];predictedPlot=Plot[n(k+1),{k,1,maxK},PlotLegends->{"n(k+1)"},PlotStyle->Gray];SF=StringForm;Show[observedPlot,predictedPlot,AxesLabel->{"k","purity"},PlotLabel->SF["Product of k n-x-n matrices with n=``",n]]
Isometry/Ahle
TLDR; information is kept on isometries, but isometry + small noise will lose it
Out[]=
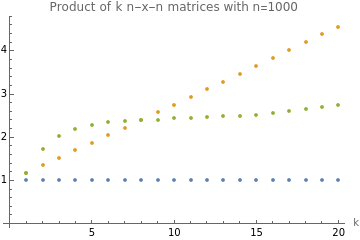
ClearAll["Global`*"];n=1000;maxK=20;relu[mat_]:=Clip[mat,{0,∞}];purity[mat_]:=With{n=Length[mat],mat2=mat.mat},;(*productsofisometries*)sample=RandomVariate[CircularRealMatrixDistribution[n]];matsIso=NestList[#.sample&,sample,maxK-1];
nTr[mat2.mat2]
2
Tr[mat2]