In[]:=
(*deployswithcanonicalname*)deploy
Wed 19 Jul 2023 17:14:16
Estimating sum of 4th powers of singular values
Estimating sum of 4th powers of singular values
In[]:=
ClearAll["Global`*"];(*originaldefinitionintermsofsingularvalues*)purity[mat_]:=With{x=SingularValueList[mat]},n;(*definitionintermsofFrobeniusnorm*)purity2[mat_]:=With{n=Length[mat]},;entriesSum[mat_]:=Total[mat,2];gramMatrix[mat_]:=Outer[Dot[#1,#2]&,mat,mat,1];(*definitionintermsofpairwisedotproductssquared*)purity3[mat_]:=With{n=Length[mat]},n;(*subsampledversion*)subsample[mat_,rows_]:=RandomSample[mat,rows];purity4[mat_,k_]:=Module{},n=Length[mat];submat=RandomSample[mat,k];norms2=Total[&/@submat];norms4=Total[&/@submat];dotProducts2=entriesSum[];averageDot2=(dotProducts2-norms4)(-k);averageNorm4=norms4k;averageNorm2=norms2k;n;purity5[mat_,k_]:=Module{},n=Length[mat];submat=RandomSample[mat,k];norms2=Total[&/@submat];norms4=Total[&/@submat];dotProducts2=entriesSum[Tr[submat.submat.submat.submat]];averageDot2=(dotProducts2-norms4)(-k);averageNorm4=norms4k;averageNorm2=norms2k;n;normal=NormalDistribution[];uniform=UniformDistribution[{-1,1}];n=100;maxK=10;sample:=RandomVariate@@{dist,{n,n}};dist=normal;matsNormal=NestList[#.sample&,sample,maxK-1];rowNormalize[mat_]:=Normalize/@mat;mats=rowNormalize/@matsNormal;purity/@matsNormalpurity2/@matsNormalpurity3/@matsNormalSeedRandom[1];purity4[#,n/2]&/@matsNormalSeedRandom[1];purity5[#,n/2]&/@matsNormal
Total[]
4
x
2
Total[]
2
x
nTr[mat.mat.mat.mat]
2
Tr[mat.mat]
entriesSum[]
2
gramMatrix[mat]
2
(Total[&/@mat])
2
Norm[#]
2
Norm[#]
4
Norm[#]
2
gramMatrix[submat]
2
k
averageDot2(-n)+averageNorm4*n
2
n
2
(averageNorm2*n)
2
Norm[#]
4
Norm[#]
2
k
averageDot2(-n)+averageNorm4*n
2
n
2
(averageNorm2*n)
Out[]=
{1.99616,3.09095,3.93699,5.31511,5.73882,6.82099,8.56259,9.33436,10.442,10.6216}
Out[]=
{1.99616,3.09095,3.93699,5.31511,5.73882,6.82099,8.56259,9.33436,10.442,10.6216}
Out[]=
{1.99616,3.09095,3.93699,5.31511,5.73882,6.82099,8.56259,9.33436,10.442,10.6216}
Out[]=
{1.97894,3.15838,3.94185,4.97614,5.2586,6.83678,8.68047,8.95716,11.1527,10.2221}
Out[]=
{1.97894,3.15838,3.94185,4.97614,5.2586,6.83678,8.68047,8.95716,11.1527,10.2221}
In[]:=
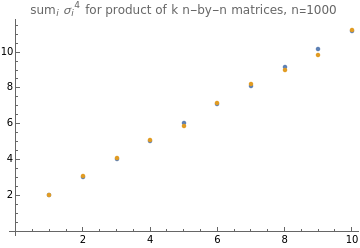
normal=NormalDistribution[];uniform=UniformDistribution[{-1,1}];n=1000;maxK=10;sample:=RandomVariate@@{dist,{n,n}};dist=normal;matsNormal=NestList[#.sample&,sample,maxK-1];SF=StringForm;ListPlot[{purity2/@matsNormal,purity5[#,n/10]&/@matsNormal},PlotLegends->{"exact","n/2 subsampled"},PlotLabel->SF[" for product of k n-by-n matrices, n=``",n,AxesLabel->{"k"}]]
sum
i
4
σ
i
Out[]=