Introduction to Quantum Optimization
Introduction to Quantum Optimization
This course provides a practical introduction to Quantum Optimization through the Wolfram Quantum Framework combined with modern quantum libraries. It explores the foundations of Variational Quantum Algorithms (VQAs), including parametrized circuits, cost functions, and optimization strategies, and advances to key methods such as the Variational Quantum Eigensolver (VQE) and the Quantum Approximate Optimization Algorithm (QAOA) for tackling problems in quantum chemistry and combinatorial optimization. Students also learn advanced techniques like Quantum Natural Gradient Descent (QNGD) and Quantum Linear Solvers (QLS), from the HHL algorithm to variational and multiplexer-based approaches.
Wolfram U Course (videos): https://www.wolfram.com/wolfram-u/courses/mathematics/wsg63-quantum-optimization/
Summary
Summary
Table of contents
Table of contents
Click on the title of each section to access the material, which combines clear explanations of the theory with practical exercises that will guide you in applying and exploring the algorithms:
◼
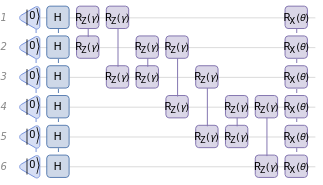
Parametrized Quantum Circuits
◼
Ansatz Circuits: How good is an Ansatz?
◼
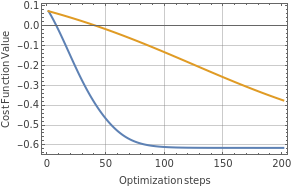
Cost Functions and Optimization
◼
Variational principle, objective and implementation
◼
Quantum Chemistry (WQF + Pennylane)
◼
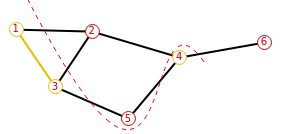
Combinational Optimization & QAOA
◼
Max-Cut Problem
◼
QAOA-in-QAOA
◼
Parameter Shift Rule, Gradient and Natural Gradient Descent
◼
Fubini-Study metric tensor & QNGD
◼
Harrow–Hassidim–Lloyd algorithm (HHL)
◼
Variational Quantum Linear Solver(VQLS)
◼
Multiplexer-Based Quantum Linear Solver