Section 3.6: Imperfect Bifurcations and Catastrophes
Section 3.6: Imperfect Bifurcations and Catastrophes
Imperfect Bifurcations and Catastrophes Cont.
OK, where were we? We have been looking at a seemingly very simple differential equation which has two parameters, and
h
r
x
3
x
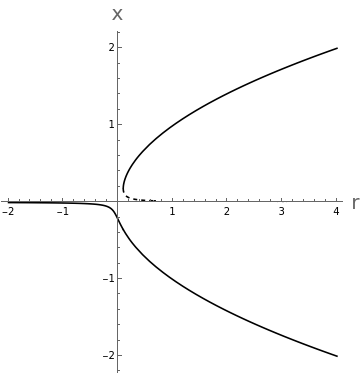
We know how to find fixed-points of a differential equation, and we have been finding these for different values of and then plotting the fixed points in on a graph as a function of . This was what we had the last time:
h
x
r
In[]:=
pl[h_]:=Module[{topl,r},sol[r_]:=x/.NSolve[h+rx-0,x];topl=If[h0,Show[Plot[0,{r,-2,0},PlotStyle{Thick,Black},PlotRange{{-2,4},{-2.2,2.2}},AxesLabel(Style[#,20]&/@{"r","x"}),AspectRatio1],Plot[0,
3
x
r
,-r
,{r,0,4},PlotStyle{{Thick,Black,Dashed},{Thick,Black},{Thick,Black}},AxesLabel(Style[#,20]&/@{"r","x"}),AspectRatio1]],Plot[Evaluate[sol[r]],{r,-2,4},PlotStyle{Black,Black,{Black,Dashed}},AxesLabel(Style[#,20]&/@{"r","x"}),AspectRatio1]];Clear[sol];topl]In[]:=
Manipulate[pl[h],{{h,0},-1,1},SaveDefinitionsTrue]
Out[]=
In this case we are changing and seeing what happens to the fixed points. We can think of this as slicing through a surface where there is a new dimension. How about plotting this in three dimensions? i.e. as the fixed points of as a function of and :
h
h
x
r
h
In[]:=
plot2=Module[{h,r,x,sol},sol=x/.Solve[h+rx-0,x]//Simplify;Show[Plot3D[Chop[sol],{r,-2,-0.01},{h,-1,1},PlotStyle{Lighter[Blue],Opacity[0.8]}],Plot3D[Chop[sol],{r,0.01,4},{h,-1,1},PlotStyle{Lighter[Blue],Opacity[0.8]}],BoxRatios1,AxesLabel(Style[#,20]&/@{"r","h","x"})]]
3
x
Out[]=
You should be able to rotate the figure to see it from all angles. Note that here we haven’t said what is a stable and what is an unstable fixed point. Do you notice anything familiar?
There is a lot going on here! Don’t worry if this isn’t making sense at all yet.
Let’s do a bit of a sanity check here. Let’s take a slice through here at, say , and see what we have:
h=0
In[]:=
plotslice=Module[{r,x,h,sol},Show[plot2,ParametricPlot3D[{r,0,x},{r,-2,4},{x,-2,2},MeshNone,PlotStyle{Opacity[0.5],Red}],ParametricPlot3D[{r,0,0},{r,0,4},PlotStyle{Black,Thick,Dashed}],ParametricPlot3D[r,0,
r
,{r,-2,4},PlotStyle{Black,Thick}],ParametricPlot3D[{r,0,0},{r,-2,0},PlotStyle{Black,Thick}],ParametricPlot3D[r,0,-r
,{r,-2,4},PlotStyle{Black,Thick}]]]Out[]=
If you look at the intersection between the plane of and the surface that we’ve just created, you will see that it gives the plot for we’ve seen before. (Make sure you rotate if you can’t see it)
h=0
h=0
And if we look at close to -1?
h
In[]:=
plotslice2=Module[{r,h,x,sol},sol[r_]:=x/.NSolve[-1+rx-0,x];Show[plot2,ParametricPlot3D[{r,-1,x},{r,-2,4},{x,-2,2},MeshNone,PlotStyle{Opacity[0.5],Red}],ParametricPlot3D[Evaluate[{r,-1,#}&/@Evaluate[sol[r]]],{r,-2,4},PlotStyle{Black,Black,{Black,Dashed}},AxesLabel(Style[#,20]&/@{"r","x"}),AspectRatio1]]]
3
x
Out[]=
or :
h=1
In[]:=
plotslice2=Module[{r,h,x,sol},sol[r_]:=x/.NSolve[1+rx-0,x];Show[plot2,ParametricPlot3D[{r,1,x},{r,-2,4},{x,-2,2},MeshNone,PlotStyle{Opacity[0.5],Red}],ParametricPlot3D[Evaluate[{r,1,#}&/@Evaluate[sol[r]]],{r,-2,4},PlotStyle{Black,Black,{Black,Dashed}},AxesLabel(Style[#,20]&/@{"r","x"}),AspectRatio1]]]
3
x
Out[]=
This strange surface that we’ve plotted looks a bit like a folded piece of cloth. Let’s look at a clearer drawing of it, taken from Steven Strogatz’s book on Nonlinear Dynamics and Chaos:
Something very interesting happens here if we want to move back in the other direction!
This means that if the parameter changes even a tiny bit, you may well find that you are never able to get back to the situation that you were in before!
OK, there’s another way of plotting all of this. Let’s look at the surface from above:
Exercise: One can model the population of insects by:
which is now a differential equation with just two free parameters. See how far you can get in showing that this also has a cusp catastrophe.
There is a nice explanation of this example here but I’d like you to have a go at it yourself first. Have a watch of it, and see if you can understand the behaviour as you change the different parameters. In particular look at around 25 minutes to see the change as you slowly increase the reproductive rate of the population and how an insect outbreak can suddenly occur.
There is a nice explanation of this example here but I’d like you to have a go at it yourself first. Have a watch of it, and see if you can understand the behaviour as you change the different parameters. In particular look at around 25 minutes to see the change as you slowly increase the reproductive rate of the population and how an insect outbreak can suddenly occur.