Section 3 exercises: Bifurcations

Complete these as you are going through part 3. Try and do questions from this regularly.
Many of these questions come from or are inspired by the questions in Strogatz - Nonlinear dynamics and Chaos.
​
1
.
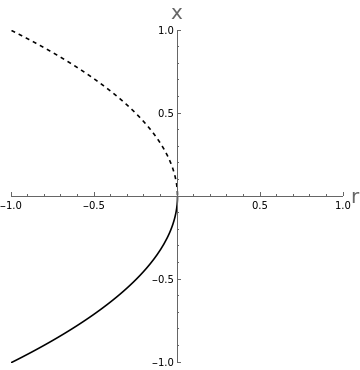
Questions on saddle-node bifurcations:​i) Sketch the different vector field types that appear when you vary
r
in the following differential equations. ii) Show that there is a saddle-node bifurcation (though there may more fixed points than just the two), and find the critical point of the bifurcation iii) and plot the bifurcation diagram. ​For instance, if you were given the equation

x
=
2
x
+r
, you would write:​i)
​ii) There is a critical point at
r=
r
c
where the stable and unstable fixed points come together after which there is no fixed point. This is the definition of a saddle-node bifurcation.​iii) The bifurcation diagram looks like:​​
​​
1
.

x
=2+rx+
2
x
(Solution including questions 2 and 3)
2
.

x
=r-cosh(x)
(Solution including questions 2 and 3)
3
.

x
=r+x-ln(1+x)
(Solution including questions 2 and 3)
4
.

x
=r+
x
2
-
x
1+x
(
Solution
including questions 2 and 3)​
2
.
For the example of the equation

x
=
2
x
+r
, plot the potential for different values of
r
and see what the behaviour looks like there in that picture.
​
3
.
We mentioned Normal Forms in the notes. The point is that close to the bifurcation point, ALL saddle-node bifurcations look like

x
=r+
2
x
or

x
=r-
2
x
.
​For instance, for the equation

x
=r-x-
-x
e
,
there is a critical point at
r
=1 at
x=0
. We can expand the right hand side close to
x=0and
it gives us:

x
=r-x-1-x+
2
x
2!
-...=(r-1)-
2
x
2
+....
Up to a scaling in
x
and a shift in
r
, this is the same as

x
=r-
2
x
.
​Go through the above equations from exercise 1 and show that when you expand around the bifurcation point, they all take on the same normal form. If you need to expand a function, you can use Wolfram Alpha, for instance, for
cosh(x):
​​
​​which you can then plug into the right hand side of

x
=r-cosh(x)
and see what happens for
xcloseto0.
​​
4
.
Now do the same thing as questions 1 and 2 for the following transcritical bifurcations:
1
.

x
=rx+
2
x
(This is the canonical example of a transcritical bifurcation (with
+
2
x
instead of
-
2
x
). Follow the logic in the notes for the original example).
2
.

x
=rx-ln(1+x)
(Solution)
3
.

x
=x-rx(1-x)
(Solution)
4
.

x
=x(r-
x
e
)
(Solution)
5
.

x
=rlnx+x-1
(Solution)
​
5
.
Now do the same thing as questions 1 and 2 for the following pitchfork bifurcations. This time also classify them as subcritical or supercritical.
1
.

x
=rx+4
3
x
(This is the canonical example of a pitchfork bifurcation but with an extra factor of 4. The method is the same as in the notes for pitchfork bifurcations, just with a scaling. Make sure that you can follow this).
2
.

x
=rx-sinh(x)
(Solution)
3
.

x
=rx-4
3
x
4
.

x
=x+
rx
1+
2
x
​​
6
.
For these flows on the line, find the value of r for which a bifurcation occurs, classify the bifurcation type, and draw the bifurcation diagram
1
.

x
=r-3
2
x
2
.

x
=rx-
x
1+x
3
.

x
=5-r
-
2
x
e
4
.

x
=rx-
x
1+
2
x
5
.

x
=x+tanh(rx)
6
.

x
=rx+
3
x
1+
2
x
​​
Homepage