Section 4.1: Linear Systems in Two Dimensions
Section 4.1: Linear Systems in Two Dimensions
Linear Systems in 2D
So far we have been confined to the line, and first order systems only. We have found a richness of behaviour, from fixed points, to bifurcations to catastrophes. But one of the big issues was that you could only ever move in one direction... and that seems like quite a constraint!
In a first order system, having position means your velocity is fixed. In many systems that one thinks of, you can choose both as initial conditions! For instance, a pendulum, you can start at any point with any velocity. This is where a first order equation falls short.
In this section we are going to make a leap into the plane (Into the world of two dimensional systems). We have to be a bit careful because a two dimensional system can mean a number of things:
1) A system in two ‘spatial’ dimensions, say and each of which depends on time and is governed by only first derivatives.
x
y,
2) A system in one dimension whose dynamics is governed by a second derivative.
3) A non-autonomous system in one dimension whose dynamics is governed by a first derivative.
All would lead to two first order differential equations (Make sure that you can see this, otherwise ask!)
All would lead to two first order differential equations (Make sure that you can see this, otherwise ask!)
The other constraint that we will have is that while we were previously looking at systems which could be non-linear, we are only going to deal with linear systems here. This means that all of the equations will be of the form:
x
y
Where are constant parameters. We can also write this as a matrix equation of the form:
a,b,candd
x
Where now
x=
,A=
x |
y |
a | b |
c | d |
This tells us that the matrix encodes all of the interesting information about our system. Every single linear first order system in the plane is encoded by a different choice of the parameters in .
A
A
The fact that the system is linear (there are no or or orterms, for instance) makes life a lot easier:
2
x
sin(x)
42
y
x
y
If you have found yourself two different solutions to such a system, then you can always add them together and that will give you a new solution. I have written about this extensively in the context of second order systems, but the logic is exactly the same here.
Let’s look at a simple example of such a system. It’s not going to look like it at first, but let’s see. Remember way back in section 1.5 we looked at the pendulum example. The equation for the pendulum was:
x
g
l
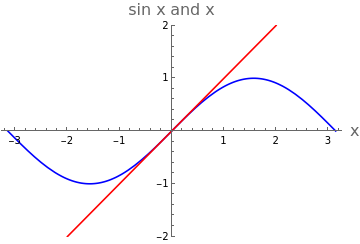
Well, this sure as anything ain’t linear, and it seems to be second order, and it seems to be in one variable... However, we can ask what happens if the pendulum only swings a bit. In that case is always small well approximated by:
x
sin(x)is
sin(x)≈x
In[]:=
Plot[{Sin[x],x},{x,-π,π},PlotStyle{Blue,Red},AxesLabel{Style["x",16],Style["sin x and x",16]},PlotRange{-2,2}]
Out[]=
So we can write the equation in the limit of small oscillations as:
x
g
l
Now if we play our trick of letting =y, then =, then we can write:
x
x
y
x
y
g
l
Which can be written as:
=
x |
y |
0 | 1 |
-g l | 0 |
x |
y |
ta-da! The pendulum in the limit of small oscillations is a first order linear system in two dimensions. Whodathunkit!
A system of this form, which stems from an equation given by
x
2
ω
is at the heart of a great deal of physics. ω here is the frequency of oscillations. This system is called the simple harmonic oscillator. In the pendulum example above, =g/l.
2
ω
Remember that in one dimension, the phase portrait was a series of arrows on the line. Well, now we can draw the phase portrait as a series of lines on the plane. The phase space is given by the plane, which we should remember is really equivalent to (but not quite the same as) the . This means that each point in the plane corresponds to a position of our ‘particle’ (or pendulum, or what have you), and its velocity. We’ve actually seen all of this back in section 1.5 Go have a read through it again to make sure that you understand.
(x,y)
(x,)plane
x
Let’s just see how to put the arrows in the plane again using our pendulum example (for small oscillations). Here is the phase plane:
In[]:=
pl1=ListPlot[{{0,0}},PlotStyle{PointSize[0]},PlotRange{{-1,1},{-1,1}},AxesLabel(Style[#,20]&/@{"x","y"}),AspectRatio1]
Out[]=
Note here that we’ve gone out to ±1 on the -axis. We should be careful because at is no longer that close to and so for anything which is that far out, we shouldn’t trust the solution completely.
x
x=1,sin(x)
x
Now let’s ask what the arrow should look like at the point... (3,1), for example. Let’s also set , so our equations are:
l=g=1
x
y
So, when and , this says that the point in our phase space will be changing its value at a rate of , and its value by a rate of . So it’s moving faster in the vertical, down direction than it is in the horizontal right direction, and we can draw in an arrow accordingly:
x=
1
2
y=
1
4
x
1
4
y
-1
2
In[]:=
Showpl1,GraphicsArrow,,,+,
1
2
1
4
1
2
1
4
1
4
-1
2
Out[]=
The arrow is actually for illustrative purposes only, so as long as the direction is right, and the relative magnitude is right, we’re ok. So let’s scale the arrow length by
1
4
In[]:=
Showpl1,GraphicsArrow,,,+
1
2
1
4
1
2
1
4
,
1
4
-1
2
4
Now see what happens as you move the point of interest around in the plane:
Now let’s plot lots of these arrows together in the plane to see the ‘flow’ of this system:
We seem to be going in circles... some sort of periodic behaviour is what you would expect for a pendulum.
Note that up until now we’ve looked at the behaviour without solving the equations at all. In fact, in this case, it’s pretty easy to solve these equations. The general solution is:
We can plot this in the plane:
Such a circle is known as a Closed Orbit which is a general type of solution which comes back to itself in phase space. Such an orbit will always correspond to an oscillatory solution.
We spoke a lot in the last sections about fixed points. Can you see whether there are any fixed points in this case?
The above example of the pendulum was a specific instance of the equation
with
Note, this is not something you should necessarily be able to see immediately by looking at the equation, but you should be able to plot the arrows. Make sure that you agree with the directions that the arrows are pointing for these five different cases.
For each case, see if you can see where the fixed points are and see if you can tell whether they are stable, unstable or half-stable.
In fact, we can look again at the equations that we are talking about here. They are:
or in other words
So we can solve this very easily and it gives us:
and plugging it into the second:
The particle moves quickly in to the centre, then slows down and will never actually arrive at the origin.