In[]:=
Sat 25 Nov 2023 23:25:15
Top level self-sufficient examples.
Depends on functions in linear-estimation-headers.nb
Depends on functions in linear-estimation-headers.nb
Random updates
Random updates
Running three different step size strategies
Running three different step size strategies
Minimizing frobenius norm
Minimizing frobenius norm
Greedy vs frobenius step sizes
Greedy vs frobenius step sizes
How does average and greedy compare?
How does average and greedy compare?
How does greedy and worst case step compare?
How does greedy and worst case step compare?
Expected error vs observed error
Expected error vs observed error
Gaussian vs Kaczmarz quantiles
Gaussian vs Kaczmarz quantiles
PyTorch port of Kaczmarz
PyTorch port of Kaczmarz
Whiten MNIST
Whiten MNIST
Fourth moment pictures and memory resurrect
Fourth moment pictures and memory resurrect
Fourth moment unit tests + production ready
Fourth moment unit tests + production ready
How two eigenvalue problems relate (stationary dist vs generalized eval)
How two eigenvalue problems relate (stationary dist vs generalized eval)
How does whitening MNIST affect test?
How does whitening MNIST affect test?
PyTorch port of Gaussian step finders
PyTorch port of Gaussian step finders
Optimal and critical Gaussian step sizes
Optimal and critical Gaussian step sizes
What is minimal L1 norm
What is minimal L1 norm
What makes a problem hard for SGD?
What makes a problem hard for SGD?
How are sample eigenvalues distributed?
How are sample eigenvalues distributed?
Activation trajectory growth/decay?
Activation trajectory growth/decay?
Parent notebook: mlc-norms-present.nb, animation-matrix-scratch.nb
Slightly cleaned-up: scratch-matrix-growth.nb
See “Free Probability” section of NN<>LeastSquares-2.nb
Slightly cleaned-up: scratch-matrix-growth.nb
See “Free Probability” section of NN<>LeastSquares-2.nb
Out[]=
Out[]=
Out[]=
Init: mlc-norms-present.nb
In[]:=
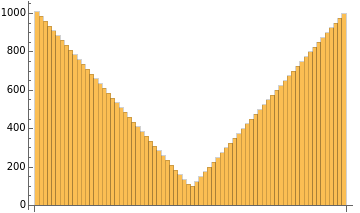
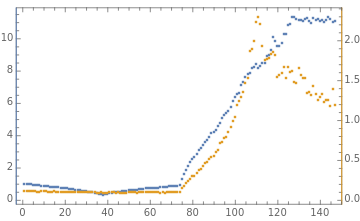
(*appliesfunctionatlevel2,ie,computeper-examplenormsoflistofbatchesofexamples*)map2[f_,l_]:=Map[f,l,{2}];(*Returnslistofactivationbatches.Side-effects:mats,xs0*)genActivations[dims0_,sampler_,normalizer_,step_,fudge_]:=Module{genMat,batchSize,dims,d0},genMat[{m_,n_}]:=fudge*normalizer@sampler[m,n];dims=Rest[dims0];batchSize=First[dims0];mats=genMat/@Partition[dims,2,1];(*initializeexamplestohavesquarednorm1onaverage*);d0=First@dims;xs0=RandomVariate[NormalDistribution[],{batchSize,d0}];normalizeLinf[mat_]:=Module{m,n,fnorm},{m,n}=Dimensions[mat];;(*randGaussian[m_,n_]:=RandomVariate[NormalDistribution[],{m,n}];*)linearStep[xs_,w_]:=xs.w;width=100;depth=10;(*numberoflinearlayers*)bs=200;upDownDims=Range[100,1010,25]~Join~Range[1010,100,-25];downUpDims=Range[1010,100,-25]~Join~Range[100,1010,25];constantDims=ConstantArray[100,74];dims=downUpDims;xs=genActivations[{bs}~Join~dims,randGaussian,normalizeLinf,linearStep,1];{normsL2,normsL1,normsLinf,absVals}=getStats[xs];is=500;TableForm[{BarChart[dims],ListPlot[{Median/@normsL2,Median/@normsLinf},Joined->{False,True},MultiaxisArrangement->All,PlotLegends->{"L2","L∞"},ImageSize->is],ListPlot[{Median/@normsLinf,Median/@absVals},MultiaxisArrangement->All,PlotLegends->{"L2","L∞"},Joined->{True,False},ImageSize->is]}]dims=upDownDims;xs=genActivations[{bs}~Join~dims,randGaussian,normalizeLinf,linearStep,1];{normsL2,normsL1,normsLinf,absVals}=getStats[xs];TableForm[{BarChart[dims],ListPlot[{Median/@normsL2,Median/@normsLinf},Joined->{False,True},MultiaxisArrangement->All,PlotLegends->{"L2","L∞"},ImageSize->is],ListPlot[{Median/@normsLinf,Median/@absVals},MultiaxisArrangement->All,PlotLegends->{"L2","L∞"},Joined->{True,False},ImageSize->is]}]dims=constantDims;xs=genActivations[{bs}~Join~dims,randGaussian,normalizeLinf,linearStep,1];{normsL2,normsL1,normsLinf,absVals}=getStats[xs];TableForm[{BarChart[dims],ListPlot[{Median/@normsL2,Median/@normsLinf},Joined->{False,True},MultiaxisArrangement->All,PlotLegends->{"L2","L∞"},ImageSize->is],ListPlot[{Median/@normsLinf,Median/@absVals},MultiaxisArrangement->All,PlotLegends->{"L2","L∞"},Joined->{True,False},ImageSize->is]}]
d0
;xs=FoldList[step,xs0,mats~Join~(Transpose/@Reverse[mats])](*FoldList[step,xs0,mats]*);getStats[xs_]:=(normsL2=map2[Norm[#,2]&,xs];normsL1=map2[Norm[#,1]&,xs];normsLinf=map2[Norm[#,∞]&,xs];absVals=Abs[Flatten/@xs];{normsL2,normsL1,normsLinf,absVals})(*Normalizationformultiplicationontheright:y=x.A*)normalizeL2[mat_]:=Module{m,n,fnorm},{m,n}=Dimensions[mat];mat
m
Norm[mat,"Frobenius"]
mat
n
Norm[mat,"Frobenius"]
Histograms
Histograms
Growth of squared norms
Growth of squared norms
Eigenvalue of iterated products
Eigenvalue of iterated products
Iterated random matrix product
Iterated random matrix product
Also see NN<>Least Squarse-2: Free probability/Convergence of Effective rank.
Rank collapses on matrix iteration. Implements random projection contours and 3D contours.
Lyapunov preconditioning doesn’t affect the spectrum but makes the matrix nicer.
Rank collapses on matrix iteration. Implements random projection contours and 3D contours.
Lyapunov preconditioning doesn’t affect the spectrum but makes the matrix nicer.
Visualize rank collapse
Visualize rank collapse
Lyapunov preconditioning
Lyapunov preconditioning
Moments of random matrices
Moments of random matrices
Main section: free-probability.nb