In[]:=
Fri 12 Jul 2024 18:45:58
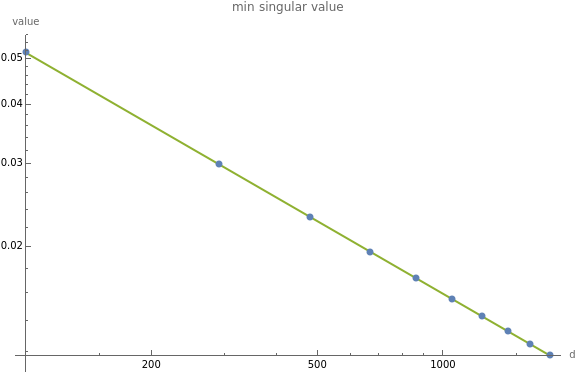
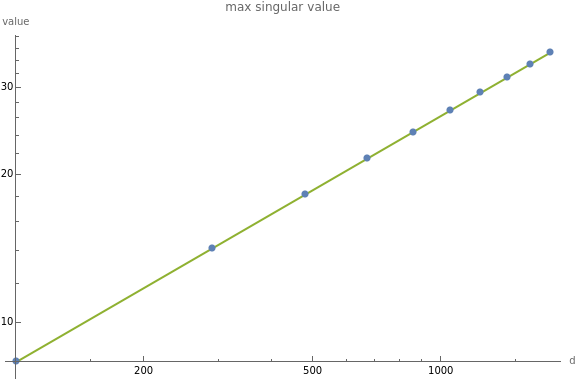
Clear["Global`*"];rowNormalize[dataset_]:=Normalize/@dataset;makeTriangularDataset[d_]:=rowNormalize@LowerTriangularize[ConstantArray[1.,{d,d}]];takeEvenly[vals_,numClusters_]:=Module[{cdfPoints,indices},(*Drop1,thelastendpoint*)cdfPoints=Most@Subdivide[0,1,numClusters];indices=Floor[Length[vals]*cdfPoints]+1;vals[[indices]]];powerLawFit[xvals_,yvals_]:=Module[{logData,linearFit,a,b,x},logData=Transpose[{Log[xvals],Log[yvals]}];linearFit=LinearModelFit[logData,x,x];{a,b}=linearFit["BestFitParameters"];fit=Exp[a+b*Log[x]];fitModel=Function@@{{x},fit};fitModel];dimsList=takeEvenly[Range[100,2000],10];minSvals=Min[SingularValueList[makeTriangularDataset[#]]]&/@dimsList;maxSvals=Max[SingularValueList[makeTriangularDataset[#]]]&/@dimsList;sf={"Log","Log"};yvals=minSvals;combinedPlot[yvals_,plotLabel_]:=(observedPlot=ListPlot[{dimsList,yvals},ScalingFunctions->sf];f=powerLawFit[dimsList,yvals];fittedPlot=Plot[{None,None,f[t]},{t,Min[dimsList],Max[dimsList]},PlotLegends->{None,None,f[t]},ScalingFunctions->sf,PlotRange->All];Show[fittedPlot,observedPlot,ImageSize->Large,AxesLabel->{"d","value"},PlotRange->All,PlotLabel->plotLabel,ScalingFunctions->sf]);combinedPlot[minSvals,"min singular value"]combinedPlot[maxSvals,"max singular value"]
Out[]=
Out[]=
In[]:=
rowNormalize[dataset_]:=Normalize/@dataset;makeTriangularDataset[d_]:=rowNormalize@LowerTriangularize[ConstantArray[1,{d,d}]];Min@SingularValueList@makeTriangularDataset[5]
Out[]=