Juegos matemáticos: Fractales parte 2 - aplicaciones, conjuntos complejos y reglas de sustitución
Juegos matemáticos: Fractales parte 2 - aplicaciones, conjuntos complejos y reglas de sustitución
por Ed Pegg
Encuentre la primera parte aquí
Este cuaderno es una traducción al español del artículo de la Comunidad Wolfram “Mathematical Games: Fractals Part 2 - applications, complex sets, and substitution rules” producido con ayuda de un LLM y verificado por un traductor profesional
Parte de una serie de presentaciones en vivo llamada Juegos Matemáticos, en la cual exploramos una variedad de juegos y acertijos utilizando Wolfram Language. En este episodio, exploramos los fractales.
Sistemas 3D deterministas libres de contexto (DOL) (por Aristid Lindenmayer, John Cicilio, Premyslaw Prusinkiewicz)
Sistemas 3D deterministas libres de contexto (DOL) (por Aristid Lindenmayer, John Cicilio, Premyslaw Prusinkiewicz)
In[]:=
Text@EntityValue[Entity["WolframDemonstration","3DDeterministicContextFreeDOLSystems"],"Caption"]
Out[]=
This Demonstration contains examples of a deterministic context-free system (DOL), a simple Lindenmayer system. Here we show some simple recursive string mappings using bracketed DOL systems. The examples used here were inspired by [1].
Esta demostración contiene ejemplos de un sistema determinista libre de contexto (DOL), un sistema de Lindenmayer simple. Aquí mostramos algunos mapeos recursivos simples de cadenas utilizando sistemas DOL con corchetes. Los ejemplos utilizados aquí fueron inspirados por [1].
Árboles k-arios regulares (por Stephen Wolfram)
Árboles k-arios regulares (por Stephen Wolfram)
In[]:=
Text@EntityValue[Entity["WolframDemonstration","RegularKAryTrees"],"Caption"]
Out[]=
In a regular k-ary tree, there are k branches from every nonterminal node. See various ways to draw k-ary trees in two dimensions.
En un árbol k-ario regular, hay k ramas que salen de cada nodo no terminal. Vea varias maneras de dibujar árboles k-arios en dos dimensiones.
Límites de la ramificación de árboles (por Stephen Wolfram)
Límites de la ramificación de árboles (por Stephen Wolfram)
In[]:=
Text@EntityValue[Entity["WolframDemonstration","LimitsOfTreeBranching"],"Caption"]
Out[]=
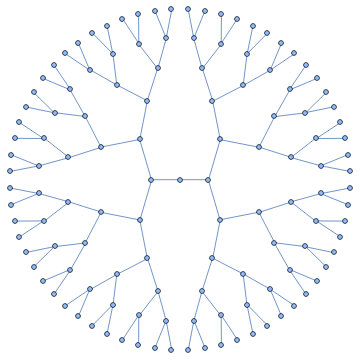
A single stem branches in two, then each branch in turn branches in two, and so on. At each step, the tips of the new branches have the same geometrical relationship to the previous branch as the first branches had to the original stem. Each dot represents the tips of branches. Vary the position of the first branch, and see the radically different limiting shapes produced.
Un solo tallo se divide en dos, luego cada rama a su vez se bifurca en dos, y así sucesivamente. En cada paso, las puntas de las nuevas ramas mantienen la misma relación geométrica con respecto a la rama anterior que las primeras ramas tenían con el tallo original. Cada punto representa las puntas de las ramas. Varíe la posición de la primera rama y observe las formas límite radicalmente diferentes que se producen.
Alfombra de Sierpinski (por Peter House)
Alfombra de Sierpinski (por Peter House)
Esta demostración recorre algunas iteraciones de la alfombra de Sierpinski, un fractal creado en 1916.
Tamiz de Sierpinski (por Peter House)
Tamiz de Sierpinski (por Peter House)
Esta demostración recorre algunas iteraciones del tamiz de Sierpinski (o junta), que fue descrito por Waclaw Sierpinski en 1915, pero apareció antes en el arte italiano.
Tipos de tamiz de Sierpinski (por Robert Dickau)
Tipos de tamiz de Sierpinski (por Robert Dickau)
Esta demostración utiliza la funcionalidad de tipografía de Mathematica para crear un tamiz de Sierpinski (o junta) mediante el anidamiento de la función Subsuperscript.
Curvas de Koch (por Michael Sollami)
Curvas de Koch (por Michael Sollami)
La curva de copo de nieve de Helga Von Koch es la curva límite de una secuencia infinita de curvas poligonales. El copo de nieve de Koch es un ejemplo de curva fractal con área finita y longitud infinita. Cambie el ángulo de la regla de actualización para crear patrones interesantes. Normalmente, la curva inicial es un triángulo o una línea, pero cualquier polígono funcionará.
Poliedros subdivididos de Koch (por Robert Dickau, Stewart Dickson)
Poliedros subdivididos de Koch (por Robert Dickau, Stewart Dickson)
Esta Demostración muestra una técnica "graftal" para subdividir las caras triangulares de un poliedro.
Muchas curvas fractales pueden generarse utilizando L-sistemas o reglas de reescritura de cadenas, en las cuales las etapas sucesivas de la curva se generan reemplazando cada segmento de línea por varios segmentos más pequeños en una disposición particular.
La misma técnica puede extenderse a las superficies, donde una etapa se construye reemplazando cada triángulo por varios triángulos más pequeños. Aquí aplicamos esta técnica a dos de los poliedros regulares con caras triangulares
Muchas curvas fractales pueden generarse utilizando L-sistemas o reglas de reescritura de cadenas, en las cuales las etapas sucesivas de la curva se generan reemplazando cada segmento de línea por varios segmentos más pequeños en una disposición particular.
La misma técnica puede extenderse a las superficies, donde una etapa se construye reemplazando cada triángulo por varios triángulos más pequeños. Aquí aplicamos esta técnica a dos de los poliedros regulares con caras triangulares
Curvas fractales de Koch cuadradas (por Robert Dickau)
Curvas fractales de Koch cuadradas (por Robert Dickau)
La curva fractal clásica de Koch se crea recursivamente comenzando con un segmento de línea y luego agregando recursivamente una flexión triangular en el centro de cada segmento. Se pueden crear variaciones utilizando una forma cuadrada en lugar de un triángulo en la regla de reemplazo. La curva de tipo 1 es una analogía directa de la curva de Koch clásica, reemplazando cada segmento de línea con cinco segmentos más pequeños colocados en ángulos rectos. La curva cuadrática de tipo 2, también conocida como la curva 3/2 y la curva de Koch de ocho segmentos, utiliza un motivo similar que reemplaza cada segmento con ocho segmentos más pequeños.
Conjunto de Cantor (por Eric Rowland)
Conjunto de Cantor (por Eric Rowland)
El conjunto de Cantor se obtiene a partir de [0,1] eliminando el tercio medio abierto y eliminando de manera iterativa el tercio medio de cada intervalo restante
Función de Cantor (por Douglas Rivers)
Función de Cantor (por Douglas Rivers)
Esta Demostración ejecuta ocho iteraciones de la función de Cantor. Puede acercarse al origen para observar la naturaleza fractal de la función.
Ejemplo de Riemann de una función continua pero en ninguna parte diferenciable (por Michael Trott)
Ejemplo de Riemann de una función continua pero en ninguna parte diferenciable (por Michael Trott)
La función de Dirichlet modificada (por George Beck)
La función de Dirichlet modificada (por George Beck)
Esta función de Dirichlet modificada tiene muchos nombres: Thomae, Riemann, popcorn, raindrop, ruler. Se define en el intervalo cerrado [0,1] como 1/q en los racionales reducidos p/q y 0 en cualquier otro caso. Tiene la curiosa propiedad de ser continua en los irracionales pero discontinua en cada racional en (0,1). En contraste, la función de Dirichlet (que no se muestra aquí) se define como 1 en los racionales y 0 en los irracionales. Es discontinua en todas partes y su gráfico monótono consiste en dos líneas borrosas.
Curva de Takagi (por Borut Levart)
Curva de Takagi (por Borut Levart)
Comenzando con un triángulo, la curva de Takagi (o Blancmange) es la suma de una serie de funciones en zigzag, cada una con la mitad de la altura de la anterior y el doble de zigzags. En el límite, la función sigue siendo continua, pero no es diferenciable en ningún punto. Mueva el control deslizante para aumentar el orden de la curva y active la casilla de verificación a continuación para mostrar la suma anterior y el paso actual de la construcción. La derivada se grafica a la derecha.
Función continua pero en ninguna parte diferenciable de Bolzano (por Izidor Hafner)
Función continua pero en ninguna parte diferenciable de Bolzano (por Izidor Hafner)
Bolzano descubrió esta función continua pero en ninguna parte diferenciable antes de 1831, pero estas investigaciones no fueron publicadas hasta 1930. Weierstrass encontró una función análoga en 1875. La función es el límite de las que se grafican cuando n∞.
Minkowski's Question Mark Function (by Oleksandr Pavlyk)
Minkowski's Question Mark Function (by Oleksandr Pavlyk)
Función signo de interrogación de Minkowski (por Oleksandr Pavlyk)
Función signo de interrogación de Minkowski (por Oleksandr Pavlyk)
La naturaleza fractal de las particiones (por George Beck)
La naturaleza fractal de las particiones (por George Beck)
Reescriba la siguiente partición de 21 como un producto punto de frecuencias y partes: 1+1+1+2+4+4+8=3×1+1×2+2×4+1×8=(3,1,0,2,0,0,0,1,0,0,0,…,0)·(1,2,3,4,…,21). La suma de las frecuencias es 7. Las particiones se enumeran en orden lexicográfico inverso. Por ejemplo, las cinco particiones de 4 se enumeran como 4, 3+1, 2+2, 2+1+1, 1+1+1+1. Para cada n, esta demostración representa (de abajo hacia arriba) las medias, medianas y sumas de las frecuencias distintas de cero de las partes de las particiones de n.
Conjuntos de Cantor generalizados y sus dimensiones de Hausdorff (por Erin K. Kline, Matthew A. Morena)
Conjuntos de Cantor generalizados y sus dimensiones de Hausdorff (por Erin K. Kline, Matthew A. Morena)
¿Qué es la no periodicidad? Teselado Pinwheel
¿Qué es la no periodicidad? Teselado Pinwheel
Isopenta
Isopenta
Teselados de Penrose y techos de Wieringa
Teselados de Penrose y techos de Wieringa
Tradicionalmente, el teselado Penrose P3 está formado por rombos delgados y gruesos. Sin embargo, al elevar los vértices en tres dimensiones, es posible forzar que todos los rombos sean congruentes. La superficie resultante se conoce como un techo de Wieringa. Debido a similitudes con los cuasicristales tridimensionales, se pueden observar triacontaedros y hexecontaedros rómbicos ocultos en el teselado.
Repiteselas
Repiteselas
Más repiteselas
Más repiteselas
¿Qué es la no periodicidad? Aún más repiteselas (orden 5)
¿Qué es la no periodicidad? Aún más repiteselas (orden 5)
Teselados aperiódicos
Teselados aperiódicos
Un conjunto de teselado es aperiódico si
1. Es posible un teselado no periódico.
2. Es imposible tener regiones o parches periódicos arbitrariamente grandes.
1. Es posible un teselado no periódico.
2. Es imposible tener regiones o parches periódicos arbitrariamente grandes.
Teselados aperiódicos -- Teselados de Robinson
Teselados aperiódicos -- Teselados de Robinson
Aperiodic tiling showing hierarchical structure, published by Raphael M. Robinson in 1971.
Adoquinado aperiódico que muestra la estructura jerárquica, publicado por Raphael M. Robinson en 1971.
Joseph Samuel Myers -- “Es una familia infinita”
Joseph Samuel Myers -- “Es una familia infinita”
Reglas de sustitución -- 1 día después
Reglas de sustitución -- 1 día después
Parches grandes
Parches grandes
Parches grandes Y o Anti-Y completos
Parches grandes Y o Anti-Y completos
Parches grandes Y o anti-Y parciales
Parches grandes Y o anti-Y parciales
Yoshiaki Araki
Yoshiaki Araki
Árbol de trialidad de sombreros
Árbol de trialidad de sombreros
Represente una porción más grande del patrón de trialidad de árboles mutuos:
Reducir, replicar, reconstruir (por Stephen Face)
Reducir, replicar, reconstruir (por Stephen Face)
En cada iteración, la imagen se reduce de tamaño por un factor de dos. Luego, la imagen se replica en cada una de las tres esquinas identificadas por los controles. Después, cada copia se transforma girándola o volteándola según lo especificado por los controles. La imagen resultante se reconstruye a partir de las tres copias más pequeñas. Tras varias iteraciones, se produce una imagen fractal.
Ejercicios recursivos II: Una paradoja (por Jaime Rangel-Mondragon)
Ejercicios recursivos II: Una paradoja (por Jaime Rangel-Mondragon)
Esta demostración produce una serie de formas basadas en el anidamiento recursivo de círculos. A medida que se repite el proceso, considere qué sucede con los círculos de interior blanco cuyos centros se encuentran sobre el mayor diámetro horizontal. Reúna todos esos círculos en familias que compartan el mismo radio. Hay 1, 2, 4, 8, … círculos en cada una de esas familias. La suma de las circunferencias de los círculos en cada familia es siempre el mismo número c. Suponga que el círculo más grande tiene diámetro 1, es decir, c=π. Entonces, al aumentar el nivel, los círculos blancos convergen hacia el mayor diámetro horizontal y la conclusión es que π=1!
Ejercicios recursivos III: Patrones de fuego (por Jaime Rangel-Mondragon)
Ejercicios recursivos III: Patrones de fuego (por Jaime Rangel-Mondragon)
Esta demostración muestra una disposición basada en la subdivisión recursiva de un triángulo para producir patrones que se asemejan a figuras similares al fuego. El código ilustra el uso de números complejos en el procesamiento de figuras geométricas.
Ejercicios recursivos IV: Repiteselas (por Jaime Rangel-Mondragon)
Ejercicios recursivos IV: Repiteselas (por Jaime Rangel-Mondragon)
Si un poliómino puede ser dividido en n copias congruentes similares a sí mismo, se llama una n-repitesela. Las repiteselas son piezas auto-similares y por lo tanto pueden considerarse fractales. Esta demostración muestra tres polióminos que son 4-repiteselas: el P-pentominó, el L-triomino y la esfinge, que es un poliamante. Al disminuir la opacidad, aparece una forma 3D detrás; al girarla, se presentan diseños arquitectónicos basados en estas formas.
Ejercicios recursivos VII: Pilas de cubos (por Jaime Rangel-Mondragon)
Ejercicios recursivos VII: Pilas de cubos (por Jaime Rangel-Mondragon)
Esta demostración muestra la apilación recursiva de cubos formando una disposición piramidal que recuerda al tamiz de Sierpiński.
Ejercicios recursivos XI: Homenaje a Escher (por Jaime Rangel-Mondragon)
Ejercicios recursivos XI: Homenaje a Escher (por Jaime Rangel-Mondragon)
Esta demostración muestra dos ejemplos inspirados en la obra "Square Limit" de Escher. Ambos rotan el motivo principal para extenderlo y llenar un cuadrado. El primer ejemplo converge hacia un cuadrado de un tamaño definido en el nivel 0, mientras que el segundo crece progresivamente hasta alcanzarlo.
LSystemPlot (por Robert Dickau)
LSystemPlot (por Robert Dickau)
SchmidtArrangements
SchmidtArrangements
Fractal de volutas
Fractal de volutas
Ghee Beom Kim
Ghee Beom Kim
Relación = 1,118, que es 1/ϕ + 0,5 donde ϕ es la proporción áurea
Preguntas sin resolver
Preguntas sin resolver
Los rombos de Penrose 2D disímiles se vuelven semejantes en un techo de Wieringa 3D. ¿Qué otras sustituciones de piezas disímiles tienen un equivalente en 3D?
¿Qué sistemas de sustitución aún no se han descubierto?
Descubrí muchas sustituciones nuevas al resolver el problema de rodear un punto 2D con triángulos semejantes. ¿Quién podrá resolver el problema de rodear un punto 3D con formas semejantes?
¿Qué sistemas de sustitución aún no se han descubierto?
Descubrí muchas sustituciones nuevas al resolver el problema de rodear un punto 2D con triángulos semejantes. ¿Quién podrá resolver el problema de rodear un punto 3D con formas semejantes?
Las patas de los geckos se comprendieron hace menos de 20 años. Funcionan mediante una aplicación fractal de fuerzas de Van der Waals. ¿Cuáles son otras aplicaciones?
CITE ESTE CUADERNO
CITE ESTE CUADERNO
Juegos matemáticos: Fractales parte 2 - aplicaciones, conjuntos complejos y reglas de sustitución
por Ed Pegg
Comunidad Wolfram, STAFF PICKS, 20 de noviembre de 2025
https://community.wolfram.com/groups/-/m/t/3578703
por Ed Pegg
Comunidad Wolfram, STAFF PICKS, 20 de noviembre de 2025
https://community.wolfram.com/groups/-/m/t/3578703