Juegos matemáticos: Fractales parte 1 - aplicaciones, conjuntos complejos y reglas de sustitución

por Ed Pegg
Este cuaderno es una traducción al español del artículo de la Comunidad Wolfram “Mathematical Games: Fractals Part 1 - applications, complex sets, and substitution rules” producido con ayuda de un LLM y verificado por un traductor profesional
Parte de una serie de presentaciones en vivo llamada Juegos Matemáticos, en la cual exploramos una variedad de juegos y acertijos utilizando Wolfram Language. En este episodio, exploramos los fractales.
Episodio de YouTube: https://www.youtube.com/live/hPEs0ardvo4

demonstrations.wolfram.com

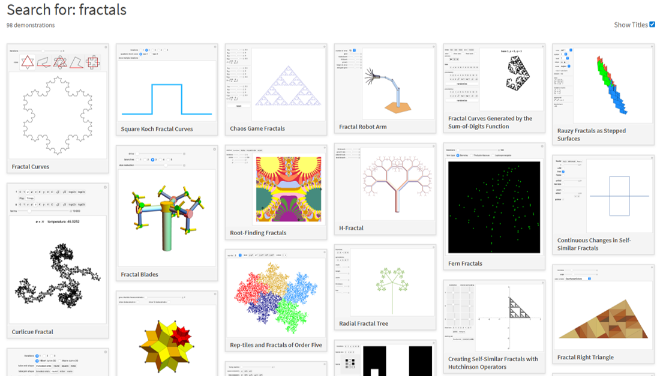
Muchas Demostraciones involucran fractales

Fractales en Gardner

Algunos de los fractales cubiertos por Martin Gardner incluyen:
Losetas de Penrose
Números surreales de Conway
Fractales de Mandelbrot
Música fractal
Código Gray binario
La curva del dragón
Repiteselas

Benoit Mandelbrot (20 de noviembre de 1924 – 14 de octubre de 2010)

La primera vez que mantuve correspondencia con Benoit fue en 1990, cuando le pedí permiso para usar el conjunto de Mandelbrot. Él respondió: “Eres el primero en preguntar. No necesitas mi permiso, es un objeto matemático. Dicho esto, tienes mi permiso.”
Más adelante, a través de periodictable.com, se puso en contacto con nosotros porque quería pedirnos prestada una de nuestras muestras de uranio, así que le enviamos una. Más adelante supimos que había dado un discurso en las Naciones Unidas sobre seguridad nuclear. Parte de su charla fue: “Vine aquí en el metro.” Luego puso un gran trozo de uranio empobrecido en el atril, en el edificio de las Naciones Unidas, y dio su charla. Después, nos lo devolvió.

Números binarios

Simplemente observar los números binarios conduce a un fractal.
In[]:=
ArrayPlot[Transpose[Table[IntegerDigits[n,2,6],{n,1,2^6-1}]]]
Out[]=
In[]:=
ArrayPlot[Transpose[Table[IntegerDigits[n,2,8],{n,1,2^8-1}]]]
Out[]=
In[]:=
ArrayPlot[Transpose[Table[IntegerDigits[n,3,4],{n,1,3^4-1}]]]
Out[]=
Por supuesto, hay fractales por todas partes.

¿Cuán larga es la costa de Bretaña? (por Jaime Rangel-Mondragon)

In[]:=
Text@EntityValue[Entity["WolframDemonstration","HowLongIsTheCoastOfBritain"],"Caption"]
Out[]=
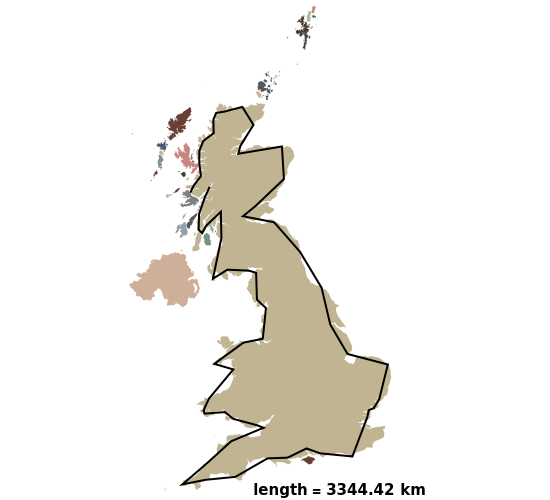
This Demonstration examines the coastline paradox, studied by Benoit Mandelbrot (1924–2010) in his influential 1967 short paper "How Long Is the Coast of Britain?" [3]. The smaller the length of the measuring stick, the longer the length of the coast appears, so that in the limit the coast of the island of Great Britain is of infinite length! Starting from an empirical law obtained previously by Richardson, Mandelbrot introduced the idea of "fractals", concluding that it is meaningless to talk about the length of a coastline and proposing a generalization of the concept of fractal dimension to measure the degree of roughness involved in such measurements.
Esta demostración examina la paradoja de la línea costera, estudiada por Benoit Mandelbrot (1924–2010) en su influyente artículo breve de 1967 “¿Cuánto mide la costa de Gran Bretaña?” [3]. ¡Cuanto menor sea la longitud de la regla de medición, mayor parece la longitud de la costa, de modo que, en el límite, la costa de la isla de Gran Bretaña tiene una longitud infinita! Comenzando con una ley empírica obtenida previamente por Richardson, Mandelbrot introdujo la idea de los “fractales”, concluyendo que carece de sentido hablar de la longitud de una línea costera y proponiendo una generalización del concepto de dimensión fractal para medir el grado de rugosidad implicado en tales mediciones.
​
refine
Más adelante, Benoit intentó averiguar: “¿Cuándo está conectado el conjunto de Julia?”

Conjuntos de Julia cuadráticos (por Stephen Wolfram)

Generación de conjuntos de Julia (por Alijah Travascio-Green)

Conjuntos de Julia y el conjunto de Mandelbrot (por Mark McClure)

Vistas ampliadas del conjunto de Mandelbrot (por S. M. Blinder)

Efecto de Droste (por Arnoud Buzing)

El efecto Droste es un tipo de imagen recursiva en la que una versión más pequeña de la imagen completa aparece dentro de la imagen completa de manera natural. En este ejemplo en particular, la imagen completa es la parte frontal de una caja de cacao, la cual también aparece como parte de la imagen en la bandeja que lleva la enfermera.

Laberinto fractal (por Ed Pegg Jr)

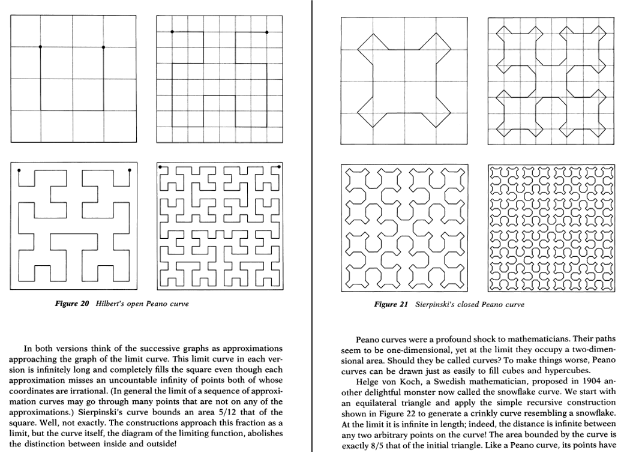
Explorador de curvas de Peano (por Robert Dickau)

Fractal H (por Sándor Kabai)

Una unidad en forma de T se ensambla a partir de tres cilindros (que representan el tronco y dos ramas de un árbol). Dos de estas unidades se colocan sobre un cilindro más grande para formar otra unidad en forma de T. Este procedimiento se repite. Puede inclinar o girar las ramas para observar el H-fractal y varias estructuras similares a árboles.

Triángulo fractal (por Sándor Kabai)

Un conjunto de triángulos equiláteros que cambian de tamaño de manera constante están conectados en sus vértices formando una estructura fractal. Puede crear el contorno de la curva de copo de nieve de Koch, entre otros patrones.

Gráficos de tortuga (por Michael Trott)

Esto demuestra una construcción basada en gráficos de tortuga de una curva que llena un cuadrado. Se le pueden dar instrucciones a una tortuga robot para avanzar o girar a la izquierda o a la derecha. El recorrido que realiza una tortuga programada, denominado gráficos de tortuga, puede dar lugar a muchas imágenes interesantes. En este caso, se le dan instrucciones a una tortuga que terminan recorriendo cada vez más partes de un cuadrado.

AnglePath (por Ed Pegg Jr)

En los “gráficos de tortuga”, una tortuga robótica lleva un bolígrafo y recibe instrucciones para avanzar o girar. La función Mathematica AnglePath hace lo mismo. Esta demostración muestra cómo esta función puede replicar varias curvas.

Inflando un dragón (por Borut Levart, Sander Huisman)

Partiendo de un cuadrado, cortamos repetidamente los polígonos en piezas y las deslizamos separándolas. El fractal del dragón emerge.

n-Copos (por Eric W Weisstein, Michael Croucher)

Se pueden crear atractivos diseños similares a copos de nieve al disponer iterativamente n n-gonos alrededor de un n-gono inicial. Un ejemplo famoso de este tipo de construcción es el pentacopo, que fue observado por primera vez por Albrecht Dürer. Esta demostración le permite experimentar con varios tipos diferentes de n-copos. El control deslizante de “factor de escala” solo afecta a los n-copos del tipo “variación 2” y controla el tamaño relativo de los n-gonos secundarios.

Triángulo rectángulo fractal (por Ed Pegg Jr)

Cualquier triángulo rectángulo puede dividirse en dos triángulos semejantes trazando la altura hacia la hipotenusa. Esta demostración divide iterativamente el triángulo más grande.

Teselado de sustitución (por Ed Pegg Jr)

El teselado de molinete divide un triángulo 1-2 en cinco triángulos rectángulos semejantes, un ejemplo de teselado por sustitución. Esta demostración muestra una variedad de diferentes teselados por sustitución. Establezca “número de pasos” como 0 para ver el sistema subyacente.

El pentágono de plástico de Vesa Timonen

Configurar estos no es trivial. Necesito mejorar mi código. El mismo color debería dar el mismo tamaño.
Debería verse más así:
Por Karl Scherer, algo similar
Silla de Ammann, usando la proporción áurea

Varias sustituciones fractales

El programa IFSTile proporciona cientos de otros irrepiteselas fractales de orden 3. Estos son solo algunos:

Irrepiteselas no fractales de orden 3

Aquí están todas las irrepiteselas de orden 3 no fractales que conozco:
1. Triángulos rectángulos (infinitos) y drafter3.
2. Cuatro rectángulos, que pueden inclinarse a paralelogramos.
3. Un conjunto infinito de cuadriláteros con dos ángulos rectos y el tritan2.
4. El pentágono irregular de Vesa Timonen.
5. Sillas de Mineyuki Uyematsu, Jun-ichi Miyoshi, Robert Ammann (y Karl Scherer) y Dale Walton.
La mayoría de los fractales aplican un paso repetidamente.
Existe un fractal autosimilar para ρ. Los números sobre las líneas verdes indican una determinada potencia de una raíz compleja de ρ.
El triángulo fractal plástico demuestra una serie infinita. Aumente las iteraciones para mejorar el fractal.

Náutilo con triángulo fractal con la razón superáurea

PsiQuad es un fractal autodefinido:
Podemos crear un fractal utilizando el juego del caos, que elige aleatoriamente el siguiente punto entre dos opciones. La iteración produce dos triángulos fractales similares.
En su lugar, podemos generar el borde ondulado hasta cualquier profundidad fractal deseada.
Ambos triángulos juntos forman un tercer triángulo similar, lo que lo convierte en una disección autosimilar, irrepitesela, o fractal de Rauzy.
Con los cuadriláteros.
Con la forma obtenemos un nautilus fractal:
Una serie de estos se cubre a sí misma.

Inicializaciones

huerto

Repiteselas (por Erich Friedman, George Freeman, Karl Scherer)

Una figura bidimensional que puede recubrirse a sí misma con n copias más pequeñas e iguales de sí misma se llama una repitesela y se dice que es rep-n. El orden de una repitesela es el número más pequeño n tal que la tesela es rep-n. Cualquier policuadrado que recubra un cuadrado es obviamente una repitesela. Estos casos triviales se omiten aquí.

Irrepiteselas (por Karl Scherer, Michael Reid, Rodolfo Kurchan, Ernesto Amezcua, George Freeman y George Sicherman)

Una figura que puede teselarse a sí misma con teselas más pequeñas de igual tamaño se llama repitesela.
Una figura que puede teselarse a sí misma usando teselas de diferentes tamaños se llama irrepitesela o irreptilo.
Esta demostración presenta 73 irrepiteselas (y sus teselados) con menos de 20 piezas en el teselado.
Adicionalmente, se proporcionan diagramas generales (del 74 al 80) que también enumeran algunas figuras de orden irregular más alto; esos teselados no se muestran aquí.

Parametrización de una curva fractal (por Cedric Voisin)

La parametrización mostrada de algunas curvas fractales conocidas es interesante porque los valores de los parámetros reflejan la jerarquía de las curvas.

Fractal de octaedro (por Ferenc Holló Szabó, Sándor Kabai)

Seis octaedros se colocan en los vértices de un octaedro mayor. Los huecos dentro del octaedro grande se rellenan con tetraedros para formar un octaedro sólido compuesto, que luego se coloca en los vértices de otro octaedro, y los huecos nuevamente se rellenan con tetraedros. Este proceso constituye dos etapas de una estructura fractal. Separe las partes en la etapa 1 o etapa 2 para ver cómo se ensambla el fractal.

Tetraedro fractal (por Sándor Kabai)

Un tetraedro se divide en cuatro tetraedros y un octaedro. Luego, cada tetraedro se divide nuevamente de la misma manera. Este proceso podría continuar para formar una estructura fractal. Una cara del tetraedro dividido se convertiría en un tamiz de Sierpinski y las partes tetraédricas 3D formarían un tetrix (o esponja de Sierpinski).

Tetraedro fractal en un octaedro (por Sándor Kabai)

Infinitos tetraedros dispuestos en una estructura fractal llenan un octaedro.

Cortes de la esponja de Menger (por Robert Dickau)

Comience con un cubo. Dibuje nueve cuadrados en cada cara del cubo, formando un patrón de 3×3. Perfore los cuadrados centrales atravesando el cubo. Tome los ocho cuadrados que quedan en cada cara y dibuje el patrón de 3×3 en cada uno de ellos. Perfore de nuevo en línea recta. Siga repitiendo ese proceso; la esponja de Menger fractal es el límite del proceso. Esta demostración corta la esponja de Menger mediante un plano perpendicular a una diagonal principal a ciertas distancias.

Esferas en un tetraedro de Sierpinski (por Sándor Kabai)

Se colocan esferas a lo largo de los bordes y en los huecos de un tetraedro de Sierpiński. Las esferas interiores forman una estructura fractal.

Tamiz de Apolonio (por Michael Schreiber)

En cada paso, inscriba nuevos discos tangentes en cada triángulo curvilíneo abierto. Estas regiones abiertas se llenan rápidamente, dejando un fractal de infinitos puntos que nunca están en ningún círculo.

Círculos de Ford con radios variables (por Ethan Zack, Jonathan Kogan)

¿Cómo se ven los teselados de ortoesquemas?

Siempre quise averiguarlo. Un primer paso es asegurarse de que el tetraedro exterior y los tetraedros más pequeños tengan la misma orientación.
Ahora podemos usar una asignación de coordenadas baricéntricas:
From that, we get the orthoscheme tiling:
A partir de eso, obtenemos el teselado de ortoesquema:
El otro ortoesquema es similar:

Sistema de sustitución definido al dividir cada celda en nueve (por Daniel de Souza Carvalho)

Se pueden encontrar patrones interesantes y anidados con un sistema de sustitución que divide cada celda en nueve celdas en cada paso. Hay 512 formas posibles de dividir las celdas blancas y negras, para un total de 262144 posibilidades. La condición inicial puede ser una celda blanca o negra, lo que duplica las posibilidades.
Este proceso genera una especie de fractal porque los resultados muestran autosimilitud. La alfombra de Haferman es uno de los patrones posibles.

Sistemas de reescritura de cadenas cartesianas binarias 2D nombradas (por Michael Schreiber)

Los sistemas de sustitución en 2D pueden utilizar diferentes matrices de tamaño 3 para reemplazar ceros y unos. Algunos de estos 262144 sistemas de reescritura de cadenas tienen nombres propios.

Evolución de sistemas de sustitución rotatorios en 3D (por Enrique Zeleny)

Experimente con sistemas de sustitución rotativos. Los controles especifican las características de dos nuevos cuadrados o cubos en relación con uno antiguo: desplazamientos en x-y, razones de tamaño r y ángulos de rotación θ. Puede ver algunos pasos de la evolución y cómo comienzan a formarse las estructuras.

CITE ESTE CUADERNO

Juegos matemáticos: Fractales parte 1 - aplicaciones, conjuntos complejos y reglas de sustitución​
por Ed Pegg​
Comunidad Wolfram, STAFF PICKS, 20 de noviembre de 2025
​https://community.wolfram.com/groups/-/m/t/3578446