On the Nature of Time and Clocks
On the Nature of Time and Clocks
David Mark Keirsey
R&D Intelligent Systems
Developing a deeper understanding of the incomplete analysis of time and clocks requires complementing them with a more sophisticated informational framework.
The nature between the concepts of time and clocks have been intertwined for millennia. This is a problem. Using the knowledge domains of science, information science, mathematics, and functional evolution, a better understanding can explicate the relationships between the two concepts in the context of the incompleteness of Einstein’s relativity and Heisenberg’s quantum mechanics, and their simplifications. The nature of physical entities and processes is more complex than mathematicians and physicists would like you to believe in the context of kinematic and inertial forms of time and clocks. The information relationships between mass, time, parity, space, linear momentum, angular momentum, and charge is explored based on the Sporadic Group Framework.
Simplifications of Relativity and Quantum Mechanics in Information
Simplifications of Relativity and Quantum Mechanics in Information
God may not play dice with the universe, but something strange is going on with the prime numbers.
-- Paul Erdős
If you don’t understand something said, don’t assume you are at fault.
-- David West Keirsey
The nature between the concepts of time and clocks have been intertwined for millennia. This is a problem. Using the knowledge domains of science, information science, mathematics, and functional evolution, a better understanding can explicate the relationships between the two concepts in the context of Special & General Relativity (SR & GR) and Quantum Mechanics (QM) simplifications. The nature of physical entities and processes are more complex than mathematicians and physicists would like you to believe in the context of kinematic and inertial forms of time and clocks. The information relationships between mass, time, space, parity, linear momentum, angular momentum, and charge can be better explicated using a more sophisticated understanding of information between physical entities and processes. Understanding of the nature of physical constants needs to be examined.
In Einstein’s analysis of Relativity, although brilliant and groundbreaking, it is incomplete. The nature of physical entities and forces is more complex than Einstein could have imagined at the time. The nature between light (Licht) and Newton’s concept of “mass” is vastly more complex in an in-form-ational sense. Einstein’s extension of the idea of Special Relativity into General Relativity (GR) clarified the dynamics of our and other star systems, but created a conceptual crack in his and Newton’s conception of gravity in the mis-match between Vera Rubin’s galaxy rotation curves versus Newton’s gravity constant and GR predictions. Physicists and cosmologists, in general, have followed in their path. Universe wide, the predictions of gravity are 95% off.
A similar analysis, much more clearly incomplete, was Bohr’s brilliant application of Planck’s and Einstein’s notions of the quanta and Lichtquant (photon). The subsequent analysis of de Broglie, Heisenberg, Schrodinger and Dirac, which is inherently statistical and probabilistic and was first understood by Max Born, is still incomplete. Statistical mechanics and Quantum mechanics has difficulty explicating phenomena such as: why three kinds neutrinos, neutrino “oscillations”, anomalous magnetic dipole moment of the muon, the missing Lithium problem, and the Gallium anomaly.
7
31
The 100 years of development of the Standard Model of Quantum Mechanics has become extremely accurate using renormalized parameters (via measured statistical “gauge and coupling constants”), but has a limited ontological basis. Correlation is not causation. With numerous, ~26, fined tuned parameters, QM is still incomplete in an information sense.
The waveforms and physical forces of physics have much more complex information content than has been assumed. Transmission of information via particles and forces varies significantly. The simple Shannon and Clausius entropy concepts used in physics models as a uniform measure is insufficient to represent the type of information transmitted in and between the waveforms and forces.
The Finite Non-Abelian Sporadic Group Framework
The Finite Non-Abelian Sporadic Group Framework
Time is everything and nothing at all.
More sophisticated information sources are needed to represent and model information transmission and exchange. The nature between “time” and “clocks” is complex especially considering effects such as neutrino oscillation, Aharanov-Bohm effect, and Jahn-Teller distortion. The following information and mathematical sources are emphasized in a more sophisticated understanding of the relationships between kinematic and inertial forms of time and clocks: Finite Simple Groups, Moufang Loops, Modular Forms, Singular Values of Primes, Parker and Non-Parker Primes.
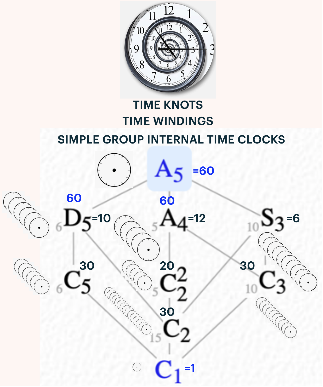
Time Knots and Internal Time Clocks
Finite Simple groups are groups that have no nontrivial normal subgroups other than the identity and the group itself. They play a critical role in understanding the concepts and percepts of: symmetry, antisymmetry, axi-symmetry, gyro-symmetry, and asymmetry. Finite Simple Groups can be seen as “time knots,” as they are “information atoms.” Groups, in general, can be seen as “time windings.” In addition, Non-Abelian Finite Simple groups can be seen as containing “internal time clocks” which are special collection of subgroups. Moreover, there are a set of special subgroups embedded in the Simple Group called “maximal subgroups” just below the group itself. Every maximal subgroup (MS) has a positive integer prime index (px) of a Simple Group G such that |G| = |MS|*px.
As a start, the Finite Simple A5 (order 60) will be used to illustrate the concepts of time knots, time windings, and simple group internal time clocks. A5 has three Prime dimensions: 2, 3, 5. Because it is a Simple Group, then it is an information atom, and a time knot. A5 is the 1st non-abelian simple group, the alternating group on 5 letters; = SL2(𝔽4) = L2(5) = L2(4) = icosahedron/dodecahedron rotations. A5 have three maximal subgroups D5, A4, and S3, with 6, 5, 10 as prime indexes respectively. That is: |A5| = |D5|*6 = |A4|*5 = |S3|*10 = 60. From an information point of view the reciprocals 1/-60, 0/-60, 0/60, and 1/60 represent a finite boolean cycle, an information atom, as a finite ordered string of bits, reminiscent of physical version of a finite Turing tape or a mRNA strand. From another informational perspective, A5 can be seen as a unique and finite automata: a Moore machine, a Mealy machine, and a Petri Net. Besides the dynamics of “time” and “clocks” physical qualia can be considered as part of this unique “informational isomorphic atom.” Finite automata qualia of length, paths, cycles, networks, space, and finite quanta (TimeSpace) can be modeled, embedded, and instantiated as part of the physical world.
In group theory, particularly in the study of finite simple groups, the index of a maximal subgroup 𝐻 in a group 𝐺 is the number of cosets of 𝐻 in 𝐺, denoted by |𝐺:𝐻| For a simple group 𝐺, the indexes of its maximal subgroups are significant because they correspond to the smallest degree of a non-trivial permutation representation of 𝐺, where the group acts transitively on the cosets of 𝐻. Hence, the maximal subgroups and their prime indexes are key in understanding the symmetries, anti-symmetries, axi-symmetries, gyro-symmetries, and asymmetries of information quanta, information atoms, information molecules and information forces.
Moufang Loops
A Moufang loop is a quasigroup (a set with a binary operation) that satisfies the Moufang identities, which is a generalization of groups. All groups are Moufang Loops.
Unlike groups, Moufang loops do not necessarily obey the associative law but maintain a weaker form of associativity through the Moufang identities: bi-associativity (a looser notion of connectivity). In some sense, Abelian and Non-Abelian Moufang Loops encompass a more informational form of a group, where the “identity element” is “fluid” within the Loop. Moreover, Non-Abelian Moufang Loops, having their left and right Bol loops that can combine to form, finitely, into open information connections of either peak or valley information gaps (up and down finite cusps of mixed or orthogonal physical qualities).
The Sporadic Groups: Mathematical “Time” and “Finite Reciprocal Prime Dimensions”
Sporadic groups are a distinct series of 27 Non-Abelian Finite Simple groups and uniqueness and intricacy are analogous to more refined versions of “time” where time here refers to the unfolding of symmetrical/asymmetrical properties and transformations of the quantum world. There are no formulas, free variables, or solutions that generate these groups: that is these 27 Finite Simple Sporadic Groups are parameterless. In other words, there are no fudge factors (or ad-hoc or post-hoc constants) in calculating the order number of these 27 unique groups. In addition, the 17 Finite Families of Non-Abelian Lie Simple Groups, on the other hand, serve as the embedding foundation for the cosmic world and the Sporadic groups Framework. At “the top and bottom” of this Framework, the Monster Group M (which represents the “information Higgs Field”) can be seen as the finite time foundation of the quantum world and as the “finite time information centers” of the main sequence stars, neutron stars, and black holes.
Sporadic groups are a distinct series of 27 Non-Abelian Finite Simple groups and uniqueness and intricacy are analogous to more refined versions of “time” where time here refers to the unfolding of symmetrical/asymmetrical properties and transformations of the quantum world. There are no formulas, free variables, or solutions that generate these groups: that is these 27 Finite Simple Sporadic Groups are parameterless. In other words, there are no fudge factors (or ad-hoc or post-hoc constants) in calculating the order number of these 27 unique groups. In addition, the 17 Finite Families of Non-Abelian Lie Simple Groups, on the other hand, serve as the embedding foundation for the cosmic world and the Sporadic groups Framework. At “the top and bottom” of this Framework, the Monster Group M (which represents the “information Higgs Field”) can be seen as the finite time foundation of the quantum world and as the “finite time information centers” of the main sequence stars, neutron stars, and black holes.
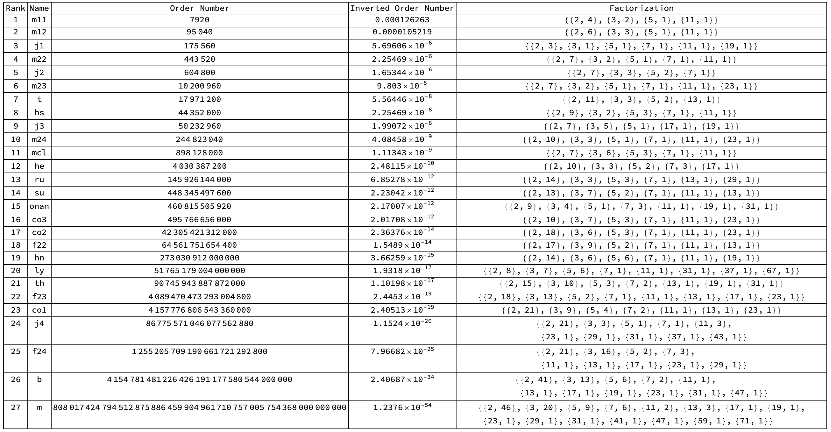
The 27 Sporadic Groups and their immediate maximal subgroup relations
In this (finite) Framework, “time” could be conceptualized as the progression through sequences of symmetrical states or transformations, each represented by finite information group actions. These group’s actions can be akin to transformations that evolve a system from one dynamic state to another, revealing symmetries/asymmetries and patterns not evident in simpler systems that rely on the simple Shannon entropy as a statistical background. This conceptual version of “time” aligns with mathematical exploration into highly structured and layered phenomena, where symmetry/axisymmetry/gyrosymmetry/antisymmetry/asymmetries play a crucial role in group and Moufang loop transformations via maximal subgroups, subgroup direct products, semi-direct, semi-simple and cyclic embeddings of “time”. In some sense, using these finite subgroups as a “semantic and finite Wick rotation” on Finite Simple Groups via time knots, time windings, and internal time clocks can model the physical world’s quantities and qualities more precisely. Besides the parameter free 27 Sporadic Groups, there are 358 maximal subgroups of the Sporadic Groups (again finite) that are encompassed precisely by the Framework (The first 20 Primes). The 15 SuperSingular Primes of the Monster group serve as encompassing and as discrete set of Riemannian manifolds of genus zero (a spherical surface).
Table 1.
There have been many proposals of physics to “include” higher dimensions (e.g., SU(5), SO(10), 11, 26), all use various forms and mixtures of Lie Algebras, Poisson Brackets, tensors, differential manifolds, and Christoffel symbols. All these constructs assume an infinite amount of information based on Newton’s and Leibniz’s calculus of the infinitesimal. (Whereas 1/|M| is a pretty small number that could be considered a finite substitute of that “elusive Planck finite infinitesimal”). The role of “mass” is treated as a “uniform” entity in the Einsteinian framework, but is super complex in the Quantum world. Mass and energy are interchanged in this context, but always assuming infinite or infinitesimal processes. The nature between “space” and “mass” is regarded as statistical and probabilistic, but Planck’s constant contradicts this view.
Sporadic Group Framework provides rich (and finite) alternative to relating mass, time, clocks, parity, and energy relative to “space” where the notion of “dimensions” is much more sophisticated and discrete. This Framework forms a Total and Partial Preorder based on Groups, Moufang Loops, Modular Forms, Supersingular Values, and Automorphisms.
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its essential (irreducible representation) network structure. The set of all automorphisms of an object forms a group, called the automorphism group. It is, loosely speaking, the symmetry group of the object. For Finite Simple Groups, the symmetries/asymmetries are directly visible via their maximal subgroups and prime indexes because Finite Simple Groups and their information embedded maximal subgroups are in some sense information atoms that correspond to physical entities, like Quantum systems as such as the electron/anti-electron, proton/anti-proton, ±muon, D± mesons, tau neutrino, Strong force and the Higgs Field.
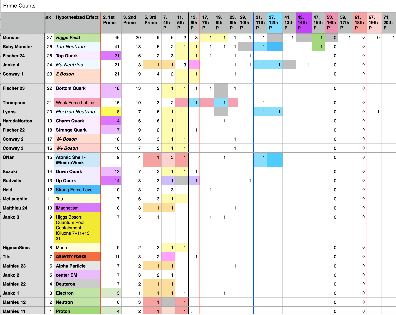
Table 2.
27 Finite Non-Abelian Sporadic Simple Groups
Modular Forms
The nature of Modular Forms is based on the Mod Function.
Modular forms are complex analytic functions that play a central role in number theory, particularly in the study of elliptic curves and automorphic forms. A modular form is a type of function that is invariant under the action of a subgroup of the modular group SL(2,), which consists of 2×2 matrices with integer entries and determinant 1. More precisely, a function 𝑓:→ (where is the upper half-plane) is a modular form of weight 𝑘 for a subgroup Γ of 𝑆𝐿(2,) if:
Modular forms can be classified by their weight 𝑘, their level (related to the subgroup Γ), and whether they vanish at cusps (cusp forms).
Supersingular Values
In the context of elliptic curves, supersingular elliptic curves are a special class of elliptic curves over fields of positive characteristic 𝑝. An elliptic curve is said to be supersingular if it has no 𝑝-torsion points, meaning the number of points on the curve over a finite field of characteristic 𝑝 is not divisible by 𝑝.
Supersingular values refer to specific values of modular functions, particularly modular forms or modular functions at supersingular 𝑗-invariants. The 𝑗-invariant is a modular function that classifies elliptic curves up to isomorphism over the complex numbers, and for each characteristic 𝑝, there is a finite set of supersingular 𝑗-invariants in the algebraic closure of the field 𝐹𝑝.
Connection between Modular Forms and Supersingular Values
Supersingular values refer to specific values of modular functions, particularly modular forms or modular functions at supersingular 𝑗-invariants. The 𝑗-invariant is a modular function that classifies elliptic curves up to isomorphism over the complex numbers, and for each characteristic 𝑝, there is a finite set of supersingular 𝑗-invariants in the algebraic closure of the field 𝐹𝑝.
Connection between Modular Forms and Supersingular Values
The connection between modular forms and supersingular values is deep and intricate. For example, the coefficients of certain modular forms (like the 𝑞-expansion coefficients of modular forms) can provide information about the number of supersingular elliptic curves in characteristic 𝑝. Furthermore, modular forms can be used to compute the supersingular 𝑗-invariants in characteristic 𝑝.
One important example of this connection is the use of the modular 𝑗-function, a specific modular function of weight 0, whose values at complex multiplication points are algebraic integers that play a significant role in the theory of complex multiplication and supersingular elliptic curves. The following table of Supersingular Values of the primes encompassed by the 27 Sporadic Group Framework are listed. The prime factors of the Monster Group are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 47, 59, 71. Two of the pariahs of the Sporadic Group: Lyons and Janko 4 besides having all of their prime factors < 71, include respectfully 31, 37, 43 and 31, 37, 67. Two prime factors embedded in the Framework, but are not prime factors of any Sporadic Group are 53 and 61. 53+61=114 which is the first number after the 30th prime 113 which contain all the p-groups.
One important example of this connection is the use of the modular 𝑗-function, a specific modular function of weight 0, whose values at complex multiplication points are algebraic integers that play a significant role in the theory of complex multiplication and supersingular elliptic curves. The following table of Supersingular Values of the primes encompassed by the 27 Sporadic Group Framework are listed. The prime factors of the Monster Group are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 47, 59, 71. Two of the pariahs of the Sporadic Group: Lyons and Janko 4 besides having all of their prime factors < 71, include respectfully 31, 37, 43 and 31, 37, 67. Two prime factors embedded in the Framework, but are not prime factors of any Sporadic Group are 53 and 61. 53+61=114 which is the first number after the 30th prime 113 which contain all the p-groups.
Table 2.
The 20 Singular Values of Prime Modular Forms encompassed by Sporadic Group Framework
Prime Parker and Non-Parker Fields
It will be illustrated that the properties of “Parker and Non-Parker Primes” help in modeling quantum properties (quantities and qualities). Matt Parker of Numberphile fame discovered an interesting mathematical pattern called Parker Squares which was almost a 3x3 Magic Square of Squares. His concept of Parker Squares was expanded upon by O. M. Cain to Parker Fields and Non-Parker Fields plus Parker Rings and Non-Parker Rings.
Information Binds and Leaks
The nature of physical entities and processes are more complex in the context of kinematic and inertial forms of time and clocks. The information relationships between physical entities and processes in terms of time, clocks, energy, mass, and space can be seen more clearly with understanding the nature of “information binds and leaks.”
The first kind (qualia) of information to address is iTime binds : iTime leaks. With the notion of Time Knots, one can view this concept as a discrete (rational valued) vector potential of a waveform, and from an informational point of view a particular kind of iTime bind. In some sense, it is a fixed point “time” perimeter (a discrete valued clock), a Simple Group (G) order number of a linear circle (a symmetric polygon). The 1st Simple Group A5 would be an example (element order: 60 sides of the polygon). An iTime leak would be maximal subgroup C of G {such that: | C | ≠ prime} of order N where | C | < | G |. As an example in A5, the subgroup S3 (|S3|=6), a maximal subgroup of A5 would be a iTime leak of 10 (the prime index). Some iTime leaks are time windings based on internal time clocks which have a “decay rate” that form the lifetime, half life, and width measures of a particle’s properties with other internal waveforms. Correspondingly, for atomic nuclei, iTime leaks are time windings based on internal time clocks which have a “decay rate” that form the lifetime, half life, and cross section measures of a nuclei’s properties with other internal waveforms. Other iTime leaks are time windings based on internal time clocks which have a “momentum rates” that form information forces internal waveforms. The Sporadic Group Framework in terms of iTime binds : iTime leaks have the maximal subgroups as sign posts for relating other kinds of information binds and leaks. See Table 3 for the first three Sporadic Groups maximal subgroups as examples. M11 represents the iProton/iAntiproton. M12 represents the iNeutron/iAntiNeutron. J1 represents the iElectron/iPositron. Just for reference, there are a total of 358 maximal subgroups in the Framework of the 27 Sporadic Groups.
Other kinds (qualia) of information relate to iTime binds : iTime leaks in different ways between iEnergy binds : iEnergy leaks; iCharge binds : iCharge leaks; iMagnetism boundaries : iMagnetism flows; iMass binds : iMass leaks; iSpin binds : iSpin leaks; and besides other qualia of higher order.
To better relate all these qualia with quantities some mathematical concepts relating to informational concepts need to be explicated. Prime Parker and Non Parker Fields and their relation to Gaussian Integers, Rings, and Magic Squares of Squares are illustrated.
Gaussian Integers
Gaussian integers are a special set of complex numbers (the second normed division algebra) that take the form 𝑎+𝑏𝑖, where 𝑎 and 𝑏 are integers. Gaussian integers are closed under addition and multiplication. The norm of a Gaussian integer 𝑧=𝑎+𝑏𝑖 is given by:
In some sense, Gaussian integers form a Normed Positive Definite Euclidean 2D Lattice (NPDEL). With the Sporadic Group Framework (maximum prime 71) this NPDEL becomes a finite lattice basis encompassed by the 15 SuperSingular Primes of the Monster Group (the Higgs Field).
Rings
Magic Square of Squares
In this particular case, the extension is over the Gaussian integers. The first Non-Parker Prime Field is 29. If one takes a certain Parker square modulo 29 one gets a 3x3 magic square of squares. The Non-Parker Prime Field 29, in some sense, is a iTime bind. In other words, the Prime Field 29 is a fixed point “time” perimeter (a discrete valued clock). Where “time” is “contained” in the perfect number 28, via the Milnor exotic 7-sphere (a boundary-less manifold) i.e., a 29 tick digital clock via Mod[x,29].
It was conjectured that the Parker Primes are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 31, 43, 47, 67. All Primes p ⩾ 71 are Non-Parker Primes. Non-Parker Primes p < 71 are 29, 37, 41, 53, 59, 61. The interesting thing about these primes is: 43 is the largest singular prime factor of information Simple Sporadic group Janko 4 (J4) which represents the Muon neutrino, 47 is the largest singular factor of information Simple group Baby Monster (B) which represents the Tau neutrino; 67 is the largest singular factor of information Simple group Lyons (Ly) which represents Electron neutrino. All three information neutrinos have the factor 31, and 31=7+11+13 which are the supersingular primes exactly encompassed by Simple group Janko 3 (J3) which represents the Higgs Boson and prime fields of 7, 11, 13 represent the information gluons.
The Standard Model of Quantum Mechanics, developed over the past century, has achieved remarkable precision through the use of renormalized parameters—specifically, statistically measured gauge and coupling constants. However, it remains limited in its ontological foundations. While it provides highly accurate correlations, these do not necessarily equate to a true understanding of causation. With around 26 finely tuned parameters, the model remains incomplete, particularly from an informational perspective.
Ever since Newton invented notion of mass (~circa 1776) and Thomas Young invented the notion of energy (~circa 1804), there has been a puzzling mystery on how these fabricated concepts relate to each other in terms of the folk notion of “time.” Einstein did an analysis (~circa 1905 and 1916) that partially illuminated their relation in the large (cosmos). However, this analysis was incomplete and only applicable to the dynamics of local star systems and not as to the galaxy as a whole.
Einstein’s analysis of special relativity starts with a gedanken experiment as an analogy to the nature of light, imagining a train going at a constant speed and two stationary observers at the opposite ends of train observing a ball dropping on a moving flat car of the train. He notes that process of the ball dropping on the train are not seen the same way (“in time”) by the observers.
Einstein analogy assumes that there is one “universal time” in the form of the “speed of light” and within an “straight-line moving object.” Implicit in the scenario is that each object (and observer) has a “one time clock” in the form of “mass” internal to themselves.
Time is considered a one dimensional “concept,” especially from a conventional physics weltanschauung. However, “space” is very much in the three dimensional Euclidean weltanschauung. With the Lorentzian invariance point of view, essentially these two world views have been concatenated together, and “mass” has been thrown in also. However, the effect of “time dilation” has two kinds of “time.” One type of time (via SR) is linear (one di-mens-ion-al). The second type of time (via GR) is more complicated, depending on the qualities of Gravity (G), Mass (M), and the measure of linear Distance (R, distance from the center of M mass). To be more specific Einstein’s equations of SR and GR are essentially based on solving two different equations:
I don’t subscribe to the bandwagon idea of the Big Bang -- Jayant Vishnu Narlikar
Einstein’s assumption is that light travels at a constant speed c in a perfect vacuum. Therefore, “nothing can go faster than the constant speed of light c in a perfect vacuum.” The first problem with this analogy is there is no such thing in our universe as a perfect vacuum. And in fact it is has been determined that “in the vacuum of space” there are “billions and billions” of electron, muon, and tau neutrinos (of unknown rest “masses”) whizzing close to the speed of light around in “space.” Using the “Big Bang model” (which uses Einstein’s field equations), Dicke et al. in 1965, surmised that “with this large matter content, the limit placed on the radiation temperature by the low helium content of the solar system is very severe. The present black-body temperature would be expected to exceed 30° K (Peebles 1965).” Dicke et. al. then adjusted their estimates to 3K post hoc, when Penzias and Wilson measured background noise (the cosmic background radiation) at approximate 3.5K. The temperature of that intergalactic “vacuum” is now measured at 2.75 degrees Kelvin. It is assumed that that “heat temperature (information)” is a result of being left over from the hypothesized “Big Bang” -- and there is no mention of the form of the “information” content other than referencing the ersatz terms “quantum foam” and “cosmic microwave background radiation (CMBR).” The Big Bang assumes that the universe started in a hot and small volume. The assumption has been there was a “slight” imbalance between “matter” and “anti-matter” in the “beginning.” No theory or direct evidence has confirmed or ruled out this highly speculative post-dict guess.
The Finite Non-Abelian Sporadic Framework supports an alternative to this guess, by realizing that from an information and mathematical perspective that “matter” and “anti-matter” are two sides of the same |G|/4 Simple Finite Group element table. E.g. the |A5| -> 4*15: (All Simple Groups have at least a factor of 4). For example, when colliding the information of electron and positron at certain linear momenta, J1: 175560 and -175560 (one gets light, usually denoted γ). In the Sporadic Framework: this is what parity is for particles. The boolean string symmetry of the Simple Group using twos-complement representation, serves as an indication of the dynamics converting mass and energy to electromagnetic radiation via “iTime merging”. |J1|=|-J1| 101010110111001000 <-> 000100111011010101
Essentially Einstein GR equations, without his cosmological constant, is a universe with a Reynolds number of 0. Einstein’s cosmological constant is an ersatz fudge factor (aka, the ersatz phrase, “Dark Energy”) to account for ~70% of the universe. The “hypothesized measure of expansion of the universe” based on General Relativity has to be suspect for missing key information concepts. Currently, (circa 2024) the problem of the “Hubble Tension” indicates there is a real problem in assuming the understanding of gravity in relation to mass and space is complete with Einstein’s weltanschauug.
The formalism of tensors in a “Hilbert space (implicitly infinite)” with Christoffel symbols as connections for Lie Algebras with Killing Vectors in a 4 dimensional space forms the mathematical background for General Relativity. However, GR and gravity are mis-matched with QM.
The Standard Model of QM is incomplete.
The existence of three leptons—the electron, muon, and tau—is a integral aspect of the Standard Model of particle physics. These particles, along with their corresponding neutrinos (electron neutrino, muon neutrino, and tau neutrino), form three generations of leptons. The reasons for their existence and why there are three generations is unknown in the physics community. The Standard Model does not provide a deeper explanation for why there are exactly three generations; it simply accepts this as an observed fact.
The electron is the lightest lepton, followed by the muon, and then the tau, which is the heaviest. The reason for this mass hierarchy is is not understood and is one of the open questions in particle physics. The different masses are thought to arise from the interactions with the Higgs field via the “quarks and gluons” SU(3).
Each generation of leptons has increasingly massive (and hence energetic) particles, but the energies (and rest masses) exhibited were discovered by measurement. Those physical measurements are ad-hoc “physical constants” (bare masses and scattering amplitudes) cobbled together using Vertex and Lie Algebras. The three generations of leptons play crucial roles in understanding the weak force, particularly in processes like beta decay and neutrino interactions. The muons from cosmic rays were decaying without being captured by atomic nuclei, contrary to what expected by the mediator of the Strong force.
It is asserted that there are three generations that allows for the phenomenon known as neutrino oscillation, where neutrinos can change from one type (flavor) to another (and “back again”?) as they propagate through space. This process requires at least three different types of neutrinos, corresponding to the three leptons. The understanding of various notions of “momentum” relative to clocks, time, mass, parity, and space needs to be better. And a new kind of “potential momentum or internal Non-Abelian momentum” should be explored.
Each generation of leptons has increasingly massive (and hence energetic) particles, but the energies (and rest masses) exhibited were discovered by measurement. Those physical measurements are ad-hoc “physical constants” (bare masses and scattering amplitudes) cobbled together using Vertex and Lie Algebras. The three generations of leptons play crucial roles in understanding the weak force, particularly in processes like beta decay and neutrino interactions. The muons from cosmic rays were decaying without being captured by atomic nuclei, contrary to what expected by the mediator of the Strong force.
It is asserted that there are three generations that allows for the phenomenon known as neutrino oscillation, where neutrinos can change from one type (flavor) to another (and “back again”?) as they propagate through space. This process requires at least three different types of neutrinos, corresponding to the three leptons. The understanding of various notions of “momentum” relative to clocks, time, mass, parity, and space needs to be better. And a new kind of “potential momentum or internal Non-Abelian momentum” should be explored.
That is, for example, quantum phenomena of Bose-Einstein condensate where fermions pass through each other indicates that quantum processes are more complicated in terms of the kinds of “internal mass/energy” and even “surface mass/energy” within the particle/waveform. The three forms of manifolds, Riemannian, Weyl, Ricci and their relationships can really have big role in clarifying the relationship between a more geometric understanding of charges ±1,±1/3,±2/3, parities, spinors, and twistors concepts. Moreover, there are 8 geometries of Thurston’s geometrization theorem which suggests that “momentum” is a complex subject both in quantity and quality.
A line integral is a type of integral that evaluates a function along a curve. It generalizes the concept of integration to higher dimensions, allowing calculation of quantities like work done by a force field along a path, mass of a wire with variable density, or circulation of a vector field. Line integrals extend the idea of integration to curves, allowing us to compute various physical and geometrical properties associated with paths in space.
I excerpted some passages from Richard Feynman’s lecture on The Schrödinger Equation in a Classical Context: (my emphasis)
“An external magnetic field is described by a vector potential, and the problem is: what are the laws of quantum mechanics in a vector potential? The principle that describes the behavior of quantum mechanics in a vector potential is very simple. The amplitude that a particle goes from one place to another along a certain route when there’s a field present is the same as the amplitude that it would go along the same route when there’s no field, multiplied by the exponential of the line integral of the vector potential, times the electric charge divided by Planck’s constant.”
mv-momentum=mv
p-momentum=mv+qA.
In the vacuum, the energy of pairing of electrons—that is, the net attraction—is very, very weak. The muon pairings and tau pairings has no net attraction in the vacuum of space, but the Sporadic Framework affords the high energy charged leptons to have a kind of fermion pairings net attraction in the main sequence stars, neutron stars, and black hole environments.
Particle/Wavicle/Wave Packet/Waveform/Force Resonances
In solid-state physics, the valence band and conduction band are the bands closest to the Fermi level, and thus determine the electrical conductivity of the solid. Between electron ionic bonds and electron valence bonds in atoms can have a range of resonances and the Fermi level serves as the finite mode threshold of the band gap.
In quantum mechanics the Schrodinger equation of the waveform is the primary formalism that is used to characterize the probability charge density and electric current density of the electron. Magnetism and electricity are pretty well understood with Maxwell’s equations, whereas the counterparts to the electron, the muon and the tau are shrouded in mystery because their lifetimes are too short and energies are too large to do exact semantic analysis. Superconductors via Bose-Einstein condensate (BEC) temperatures and regimes, the simple notion “atomic” (Newton’s billiard balls analogy) of “protons and neutrons” and the electron charges starts blur (through “higher” information binds).
Nucleons interacting with the Strong Force and the Weak Force “creates” the full periodic table with isotopes and isobars, where the “magic number” idea of Maria Goeppert Mayer tried to capture a more refined model of nucleus from the “liquid drop” model. In conventional nuclear physics, a magic number is a number of nucleons (either protons or neutrons, separately) such that they are arranged into complete shells within the atomic nucleus. As a result, atomic nuclei with a “magic” number of protons or neutrons are much more stable than other nuclei. The seven most widely recognized magic numbers as of 2019 are 2, 8, 20, 28, 50, 82, and 126. The difference between known binding energies of isotopes and the binding energy as predicted from the semi-empirical mass formula. Distinct sharp peaks in the contours appear only at magic numbers.
Magic numbers are typically obtained by empirical studies; if the form of the nuclear potential is known, then the Schrödinger equation can be solved for the motion of nucleons and energy levels determined. Nuclear shells are said to occur when the separation between energy levels is significantly greater than the local mean separation.
In nuclear physics, double beta decay is a type of radioactive decay in which two neutrons are simultaneously transformed into two protons, or vice versa, inside an atomic nucleus. As in single beta decay, this process allows the atom to move closer to the optimal ratio of protons and neutrons. As a result of this transformation, the nucleus emits two detectable beta particles, which are electrons or positrons.
There needs to be a better understanding of the information content of the waveform relative to the “particles” and “forces” other than probabilistic or statistical properties. Harmonic analysis such as the Klein-Gordon equation use wave functions, but at higher energies and velocities the details of the information resonances between particles, wavicles (wave packets), waveforms, “force carriers”, and forces cannot be modelled exactly. The weak force and beta decay are in the center of this problem, ever since Madame Wu demonstrated its complicated CPT asymmetry.
Understanding of the beta decay process was developed over decades and decades, with the initial understanding of Enrico Fermi and colleagues starting at the “superficial” first level in the diagram below. Current understanding of weak processes rest at the fourth level, at the bottom of the chart, where the nucleons (the neutron and its successor proton) are largely ignored, and attention focuses only on the interaction between the two nucleon quarks [Up and Down] (Gell-Mann concept models) and a charged boson, with the decay of the boson almost treated as an afterthought. Because the charged weak boson (W−) vanishes so quickly, it was not actually observed during the first half of the 20th century, so the diagram at level 1 omits it; even at present it is for the most part inferred by its after-effects.
Current Inferred model decay of a neutron by the Weak Force
Information and Exformation densities
Information and Exformation densities
Form-ation densities
Within an entity (i.e., within a “space”[manifold]) in the focus (e.g., waveform and/or forces) there is many kinds of qualia and quantities. The qualia (e.g., spin, magnetism, charge, energy, mass, work) within the entity have different quantity densities. In-forms (volume “Riemann” manifolds) have their dynamic densities and Endo-forms (surface “Weyl” manifolds) have their dynamic densities. In this context there are Ex-forms (volume “Ricci” manifolds) which serve as forms that act as the immediate environment for the entity.
The Information Nature of the Weak Force
In this context, the Sporadic Group Framework provides a unique insight into the informational nature of the weak force, bypassing the need for ad-hoc Lie Algebra based quantum numbers. The Framework affords the existence of only three neutrinos. and hints that neutrinos are inherently Majorana particles. This ansatz hinges on an information based understanding of the Majorana equation, which describes fermions that are their own antiparticles, emphasizing the unique role of neutrinos in the weak force.
In this context, the Sporadic Group Framework provides a unique insight into the informational nature of the weak force, bypassing the need for ad-hoc Lie Algebra based quantum numbers. The Framework affords the existence of only three neutrinos. and hints that neutrinos are inherently Majorana particles. This ansatz hinges on an information based understanding of the Majorana equation, which describes fermions that are their own antiparticles, emphasizing the unique role of neutrinos in the weak force.
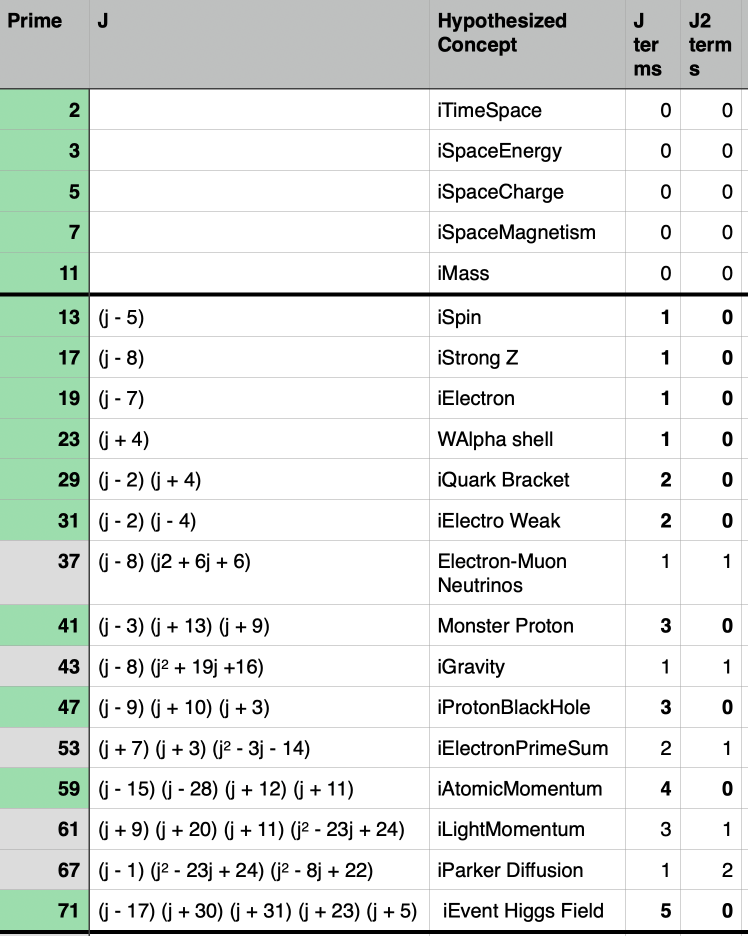
The significance of the prime 23, representing a Parker Prime and the WAlpha shell supersingular prime, underscores the relationship between the three gauge bosons (Z [Co1], W⁻ [Co2], W⁺ [Co3]) and the intricate tapestry of their interactions. Using the notion of an information vector potential the various relationships between the Sporadic Groups, one can better understand the interactions.
The significance of the prime 11, iMass supersingular prime, representing a Parker Prime, underscores the relationship between the two nucleons, iProton [M11] and iNeutron [M12] in relation to the iMuon [HS] and iTau [McL] and the intricate tapestry of their interactions. Using the notion of an information vector potential the various relationships between these Sporadic Groups, one better understand the interactions.
The significance of the prime 31, representing a Parker Prime and the iElectro Weak force, underscores the relationship between the three neutrinos (Electron Neutrino [Ly], Muon Neutrino [J4], Tau Neutrino [B]) with the Weak Force Lattice (Th) and the intricate tapestry of their interactions.
The significance of the prime 13, the iSpin supersingular prime, representing a Parker Prime and Parker Field underscores the relationship between the three lowest energy quarks (Up Quark [Ru], Down quark [Suz], Strange Quark [F22]) and the intricate tapestry of their interactions. Gell-mann’s Eight fold symmetry mirrors this relationship. Moreover, the iGravity center [T] is also intimately involved. Using the notion of an information vector potential of these various relationships between the Sporadic Groups, one better understands the interactions.
The significance of the prime 17, the iStrong-Z supersingular prime, representing a Parker Prime and Parker Field but also underscores the relationship between the Higgs Boson and the Strong Force (Higgs Boson [J3], Strong Force [He]) and the intricate tapestry of their interactions.
The significance of the prime 19, iElectron supersingular prime, representing a Parker Prime and Parker Field, underscores the relationship between the (iElectron [J1], the Higgs Boson [J3], Electron Weak Atomic Shell [ONan], Weak Force Shell [Th], Charm Quark [HN]) and the intricate tapestry of their interactions. Moreover, the iGravity center [T] is also intimately involved. Using the notion of an information vector potential of these various relationships between the Sporadic Groups, one better understand the interactions.
The significance of the prime 29, the iQuark Bracket supersingular prime, representing the first Non-Parker Prime and Non-Parker Field that underscores the relationship between the Up Quark [Ru] and Top Quark [F24’] in relation to other four quarks: Down [Suz], Strange [F22], Charm [HN], Bottom [F23]. Given that the prime field of 29 is in some sense a iTime bind, the atomic nucleus is locked down and stable except for the Weak Force and the Electro Weak Atomic Shell. The four intermediate quark energies are bracketed in between the lowest energy Up Quark and highest energy Top Quark. There are two more complex direct connections to this prime field that ultimately has a role in the information vector potentials of all of the quarks. The muon neutrino [J4] and the Higgs Field [M] have the prime factor of 29. The effects of these connections hints of many other phenomena besides the Weak Force, to be examined in other analysis.
Eventually, Epsilon normed algebras can be used to explore transformations of algebras and groups, leading to insights their stability and robustness in modelling the dynamic physical constants of the universe. Using Finite Non-Abelian Sporadic Groups as framework for embedding information into these algebras, they can be relevant in theoretical physics, where deviations from exact symmetries open up to exact anti-symmetries, axi-symmetries, gyro-symmetries, and asymmetries of the quantum and cosmic worlds.
In summary, the intricate relationships among groups and maximal subgroups of the Framework and the application of the Majorana equation not only deepen our understanding of neutrinos and their role in the Weak Force but also highlight the potential for Sporadic Group Framework that will transcend the limitations of the Standard Model. The exploration and analysis of these concepts and percepts within the Framework promises to unveil further functional patterns of the quantum and cosmic realms, integrating the information nature of waveforms, wave packets, and forces into our understanding of the universe.
References
1
.Modular Functions of One Variable, Lecture notes in mathematics 320, QA 3 L2, no 470, Table 6, SuperSingular Values, pages 143-144.
2
.Keirsey, David, “The Nature of Physical Constants” Web Resource. https://www.wolframcloud.com/obj/keirsey/Published/Ontology%20of%20Physical%20Constants.nb.
Selected Bibliography
1
.The Finite Simple Groups, R.A. Wilson, Graduate Texts in Mathematics 251, Springer, 2009.
2
.The Cosmic Revolutionary’s Handbook, Luke A. Barnes & Geraint F. Lewis, Cambridge University Press, 2020.
3
.Lost in Math, Sabine Hossenfelder, Basic Books, 2018.
4
.On Quaternions and Octonions, John Conway and Derek Smith, A K Peters/CRC Press, 2003.
5
.Symmetry and the Monster, Mark Ronan, Oxford University Press, 2006.