On the Nature of Physical Constants
On the Nature of Physical Constants
David Mark Keirsey
R&D Intelligent Systems
Towards a better ontology of quantities, measures, metrics, and Information.
The current concept of a physical “constant” is too simplistic in the quantum and cosmic realms. Physics’ reliance on Lie Groups and Lie Algebras to justify statistical Gauge theories, breaks down because of the singular fact that the honorary 27th Finite Simple Sporadic Group, the Tits Group, is a Non-Lie Simple Group. This “informational” fact relative to the notion of modular forms invalidates the general assumption that Wilson loops form a smoothly connected background representation of the concept “spacetime.” Using the knowledge domains of Science, Information Science, Mathematics, and Functional Evolution, the notion of physical constants is clarified to encompass a more explicit and finite understanding of the relationship between our universe and the nature of physical laws. A better Framework for understanding of physical concepts using information concepts such as the Finite Non-Abelian Simple Groups and Information dynamics is outlined to characterize more complex relationships and a more precise integration between models of the world and physical reality.
On the ontology between “physical constants” and “information constants”
On the ontology between “physical constants” and “information constants”
Conventional Physics Constants
Conventional Physics Constants
The idea of physical constants in physics refers to “quantities” that are “universally constant” in nature, such as: c, the speed of light in a “vacuum,” the “gravitational” constant G, and Planck’s constant h. These constants have helped our understanding of the physical universe, playing crucial roles in equations that describe the current theories of the laws of electromagnetism and gravity. The problem is G, Newton and Einstein’s “gravitational constant,” does not explain 95% of cosmos. And ℏ, “Planck’s reduced constant” is really at least three “constants” of different qualities that haven’t been “measured” directly -- being a hypothesized combination in a “continuum of relations” between “Planck mass”, “Planck length”, and “Planck time”, and assuming there is numerical equivalence relation between “Planck energy” and “Planck mass.” given the “constant c”. On the other hand, Planck’s reduced constant is discrete and finite in information. Planck interpreted [the vibrational energy of N oscillators] not as a continuous, infinitely divisible quantity, but as a discrete quantity composed of an integral number of finite equal parts.
U
N
These various “physical constants” are treated as numerical values in equations like Schrodinger’s and Einstein Field Equations in the form of “real numbers” , the Normed Division Algebra of one dimension. However, the mathematical notion of the “real number” has some epistemological problems that has plagued science and mathematics for millennia, ever since individuals like Zeno, Weierstrass, Piano, Cantor, Zermelo, Olbers, Hilbert, von Neumann, Hawking, and Witten have tried to resolve these paradoxes in and between mathematics and science. The notion of the reification of irrational and transcendental “numbers” within the “reals” needs to be questioned. Moreover, a more integrated and informational approach is outlined here comparing the conventional view with a more integrated perspective, Gestalt Science, and more specifically Gestalt Physics, that uses knowledge from Science, Information Science, Mathematics and Functional Evolution to model physical processes.
The Conventional Physical Constants and Their Role
1. Speed of Light c: Central to the theory of relativity, defining the maximum speed at which information or matter can travel in the ideal notion of the vacuum. However, the concepts of mass and information are not explicitly and singularly defined. Moreover, the ideal notion versus the actual dynamics of the “vacuum” have plague physics to this day.
2. Gravitational Constant G: Newton’s law of gravitation, relating the gravitational force between two masses to their separation. However, using Einstein field equations with G, about 95% of the observable universe is not explained and about 25% of that is “missing mass”, even though nobody can precisely define the concept of mass.
3. Planck’s Constant h: Essential in quantum mechanics, linking the energy of a photon to its frequency in a statistical manner. However, quantum mechanics using “numbers” in the form of Complex numbers, assumes that these “numbers” (particularly, one special “number” form of Normed Division Algebras) can capture enough information about the laws of nature to resolve ersatz concepts of current physics of “dark matter” and “dark energy.”
Complexities in Quantum and Cosmic Realms
In the fields of quantum mechanics and cosmology, the notion of these constants can become less than straightforward. Moreover, the mismatch between QM and GR, have created a set of paradoxes that cannot be resolved by the simplistic and misleading assumptions that these areas of conventional physics have implicitly, posited by many, as conventional wisdom and/or “truths.”
- Quantum Mechanics: At very small scales, phenomena often defy predicted expectations, leading to the need for many hypothesized physical “constants” (renormalized via experimental statistical measures) like h, (the rest “mass” of the electron), and the Higgs Boson mass, to describe the probabilistic and statistical nature of particles and waves. Without an overarching Framework, the Standard Model has been cobbled together in the last hundred years, glued together by “renormalized constants” (e.g. scattering amplitudes and “bare” masses) measured statistically to hone in on “gauge fields” via ad-hoc Taylor series expansion cutoffs (ala, Feynman “vertex” diagrams).
- Quantum Mechanics: At very small scales, phenomena often defy predicted expectations, leading to the need for many hypothesized physical “constants” (renormalized via experimental statistical measures) like h,
e
0
- Cosmology: At cosmic scales, the interplay of forces and the structure of “space-time” can make constants appear to vary, particularly when considering speculative models like quantum loop gravity, string theory, or the ersatz concept of the multiverse. Einstein’s field equations rely on tensor calculus, and tensors further rely on the concept of “real number” line and differential calculus. Ever since, Vera Rubin showed that Einstein’s field equations cannot account for galaxy rotation curves via Fisher-Tully relation, cosmology has been in the dark about what do about it.
With the total mismatch and incompleteness of General Relativity and Quantum Mechanics, a better understanding more integrated notions: e.g., “time-space”, “space-energy”, “energy-charge”, “charge-magnetism”, “magnetism-mass”, “mass-spin”, and other physical and information notions are needed. The concepts of measures and metrics are not as simple as mathematicians and physicists would like.
The Gestalt Physics Perspective
The Gestalt Physics Perspective
A number is not always a simple concept. The nature of a physical constant, a “quantity,” is also wrapped up with “qualities” in the form of “properties” and/or “factors and ratios.” Different kinds of numbers, the standard mathematical number systems are numerous: Cardinal numbers, Ordinal numbers, Whole numbers, Integer numbers, Rational numbers, Algebraic Numbers, Transcendental numbers, Real numbers, Normed Division Algebras (Real: , Complex: , Quaternion: , Octonion: “numbers”), and Clifford Algebras (e.g. Sedenions: ) are the principle examples. Physical qualities, like length, depth, time, spin, charge are in complicated relationships in the realms of the small (quantum) and large (cosmic).
Algebraic structures, besides “number systems” like the “reals,” particularly Groups, can be used in modeling Physical constants and Information constants. Information constants can be more explicit in the relationships between quantities and qualities. The Finite Simple groups are a key to better and more explicit understanding of these information constants and their relationship to the physical constants.
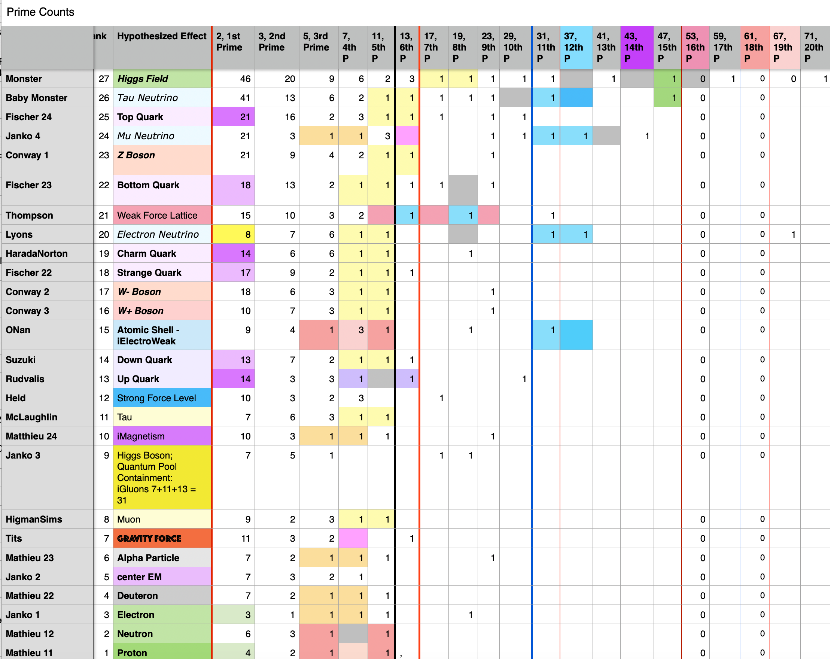
For instance, every cardinal number in the form of the order number of elements of a group and can represent one or more information concepts or physical entities. As examples, the cardinal number, 36, can represent 14 different concepts based on the 14 different groups of order 36. The first Finite Simple Group, A5, has the order of 60 group elements represents the icosahedron/dodecahedron rotations. Moreover, A5 is involved (embedded) in many other Finite Simple Groups. The other 12 of the 13 Groups of order 60 can also represent other related concepts. As it turns out, the 27 Finite Non-Abelian Sporadic Simple Groups form an information pre-order lattice that can be used as a Finite In-form-ation Framework. For example, A5 is a maximal subgroup of one of Sporadic Groups: Janko 2. See appendix for the 27 Sporadic Simple Groups and their factorization. For more analysis of this Framework refer to the article On Nature of Time and Clocks
Mathematical and Informational Structures: Finite Simple Groups, Moufang Loops, Finite Mathematical and Informational Sequences, and Information Physical Dynamics.
To understand the deeper nature of these “physical constants”, we can explore mathematical and informational structures such as Finite Simple groups and Moufang loops, which will provide an intellectual framework for informational and physical relations of symmetry, anti-symmetry, axi-symmetry, gyro-symmetry, asymmetry and other geometric algebra properties. The notion of “informational constants” in relation to “physical constants” is illustrated.
In that light, there are many kinds of groups: Direct Products (denoted by x) of groups and Group extensions of groups. Group extensions are either split-extensions or non-split extensions. The split-extensions are Semi-Direct product groups (usually denoted ⋊). Non-split extensions (usually denoted .) include either central extensions: Central Product groups (usually denoted ○) or Central Stem Product groups (aka Wreath products, usually denoted ≀).
G
1
G
2
G
1
G
2
G
1
G
2
G
1
G
2
G
1
G
2
The Finite Non-Abelian Simple groups are special in that they can serve as information quanta, information atoms, information molecules, and information forces. The infinite family of primes are in the form “information quanta” of Finite Abelian Simple Groups. The 17 Finite Non-Abelian Lie Simple Family of groups can represent physical and informational concepts of both a precise quantity and several precise qualities in precise ratios. Finally, and most importantly from an informational point of view, the 27 Finite Sporadic Simple Groups (Unique, Non-Abelian) and their 358 maximal subgroups, form a Finite Total Preorder Framework. Moreover, the 15 SuperSingular Primes form a partial ordered lattice Preorder Framework to model the universe and its processes. This Framework has no parameters to it: there are no ad-hoc fudge factors to over fit the data, unlike String Theory which have an infinite set of ad-hoc parameters to choose from.
In addition, the Moufang Loops, which are a generalization of groups, provide a more fluid and dynamic notion of identity, where both more qualitative and quantitative notions of internal or external shear forces, stresses, strains in relation to time, energy, charge, magnetism, mass, spin, angular momentum, linear momentum, and other physical concepts can be explicated.
1) Finite Simple Groups
- Brief Explanation: These are groups that have no nontrivial normal subgroups other than the identity and the group itself. They play a critical role in understanding the concepts and percepts of: symmetry, antisymmetry, axi-symmetry, gyro-symmetry, and asymmetry.
- Brief Explanation: These are groups that have no nontrivial normal subgroups other than the identity and the group itself. They play a critical role in understanding the concepts and percepts of: symmetry, antisymmetry, axi-symmetry, gyro-symmetry, and asymmetry.
- Properties: Finite simple groups play a crucial role in understanding the structure of all finite groups. Any finite group can be decomposed into a series of normal subgroups, where each quotient is a simple group. Hence, finite simple groups can be thought of as the fundamental building blocks of finite groups and fundamental building blocks of “information atoms (aka, quanta)” and “information forces (aka, qualia).” Using the fractional Rational form of the number of elements of the group, quantitative and qualitative information can be represented. E.g., 1/|G| and -1/|G| represents the “atomic” information of the Group G.
- Relevance: In the context of physical constants, Simple Finite groups can help in describing the symmetries and asymmetries of wave forms, forces, “particles” and fields. The Standard Model of particle physics relies heavily on some group properties and Lie Algebras to describe the interactions of wave functions. However, conventional particle physics being confined to the computational formalism of the second normed division algebra (complex numbers) limits the representation of the physical constants to statistical and probabilistic quantities and qualities, hiding the ability for more precise and delineated concepts and percepts of physical laws. The assumption of the differentiable continuity (implicitly assuming the infinitesimal [infinity]) of the Wilson Loops in the background “spacetime” is flawed because of their dependence of Lie Algebras [and implicitly the Poisson Bracket]. Tits Group (the honorary “27th” Sporadic Group) being the unique Finite Non-Lie Simple Sporadic Group, in some sense, “breaks” the hypothesized “spacetime” symmetry.
2) Moufang Loops
- Brief Explanation: A Moufang loop is a quasigroup (a set with a binary operation) that satisfies the Moufang identities, which is a generalization of groups. All groups are Moufang Loops.
- Brief Explanation: A Moufang loop is a quasigroup (a set with a binary operation) that satisfies the Moufang identities, which is a generalization of groups. All groups are Moufang Loops.
- Properties: Unlike groups, Moufang loops do not necessarily obey the associative law but maintain a weaker form of associativity through the Moufang identities: bi-associativity (a looser notion of connectivity). In some sense, Abelian and Non-Abelian Moufang Loops encompass a more informational form of a group, where the “identity element” is “fluid” within the Loop. Moreover, Non-Abelian Moufang Loops, having their left and right Bol loops that can combine to form, finitely, into open information connections of either peak or valley information gaps (up and down finite cusps of mixed or orthogonal physical qualities).
- Relevance: In physical theories, particularly in the study of quantum “matter” and quantum “forces” Moufang loops provide a more understandable and finite way to explore informational structures and processes (e.g., finite stress or strain), where group theory doesn’t always give clarity.
3) Finite Mathematical and Informational Integer Sequences
- Brief Explanation: An infinite integer sequence is a list of integers that continues indefinitely, with no end. Each integer in the sequence is called a term, and the total number of terms is infinite. The sequence is often written in the form {,,,,,} suggests its continuation with ellipses. A finite integer sequence is a sequence of integers in the form {,,,,,} where 𝑛 is a finite positive integer representing the total number of terms in the sequence. One can always use a finite number of terms from an infinite integer sequence to extract information from the sequence to better understand what mathematical, informational, and/or physical model that the sequence represents. In some sense, this technique of examining a finite part of infinite sequence is similar to the physicist’s ersatz method of gauge cutoff of a Taylor series.
- Brief Explanation: An infinite integer sequence is a list of integers that continues indefinitely, with no end. Each integer in the sequence is called a term, and the total number of terms is infinite. The sequence is often written in the form {
𝑎
1
𝑎
2
𝑎
3
𝑎
4
𝑎
5
...
𝑎
1
𝑎
2
𝑎
3
𝑎
4
𝑎
5
...,
𝑎
n
- Properties: Integer sequences are numerous based on the Oeis.org website. Understanding the prime factorization of some of these sequences gives clues to the nature of underlying information patterns. These sequences can model informational, algebraic, geometric, topological, and/or physical properties. There are broadly three kinds of sequences based on whether a sequence is essentially recursive, iterative, or uniquely informational in its nature. For example: 1) Number of series-reduced trees with n nodes (homeomorphic reduced trees), 2) Fermat primes, 3) normalized inverse radius of the inscribed circle that is tangent to the left circle of the symmetric arbelos and the n-th and (n-1)-st circles in the Pappus chain (epic circles), 4) The 15 supersingular primes: primes dividing order of Monster simple group. The website lists numerous well know sequences like Pascal’s triangle, Bernoulli numbers, Perfect Numbers, Mersenne primes, Catalan numbers, etc...
- Relevance: In physical theories, particularly in the study of quantum and cosmic “matter” and “forces” these integer sequences provide a different way and finite way to explore informational structures and processes (e.g., finite stress or strain), where group theory and self contained algebraic structures don’t give as much clarity. The knowledge domains of information science, material science, solid state physics, combinatorics, modular forms, and functional evolution can help selecting key sequences that model important physical and information processes.
4) Information Physical Dynamics
- Brief Explanation: Information Physical Dynamics is a set of mathematical and information sources: Formulas, Equations, Modular Forms of one variable, Epsilon Normed Division Algebras. Formulas include Integer formulas and unique kinds of mathematical equations such as the generalized quaternion. Modular Forms of one variable explicate the internal structure of primes in the form of Singular Values. See Table 1 below. Epsilon Normed Division Algebras can be used to explore transformations of algebras, leading to insights their stability and robustness in modelling the dynamic physical constants of the universe.
- Brief Explanation: Information Physical Dynamics is a set of mathematical and information sources: Formulas, Equations, Modular Forms of one variable, Epsilon Normed Division Algebras. Formulas include Integer formulas and unique kinds of mathematical equations such as the generalized quaternion. Modular Forms of one variable explicate the internal structure of primes in the form of Singular Values. See Table 1 below. Epsilon Normed Division Algebras can be used to explore transformations of algebras, leading to insights their stability and robustness in modelling the dynamic physical constants of the universe.
- Properties: Integer formulas like the taxi cab formulas, particularly Elkies taxi cab power of 5 formula, are key to understanding the information structures embedded in the 26 Non-Abelian Lie Sporadic Groups and 1 Non-Abelian Non-Lie Group (the Tits Groups). For example, the number of elements of quantitative relationship between the Simple Sporadic Groups Fischer 22 Group (F22) and Suzuki Group (Suz) is 144 (| Suz | * 144 = | F22 |). The Suzuki Sporadic Simple Group represents the information center of the down quark and the Fischer 22 Sporadic Simple Group represents the information center of the strange quark. See Appendix Table 3. Of note also, 84 is the limit superior of the largest finite subgroup of the mapping class group of a genus 𝑔 surface divided by 𝑔. A hepteract is a seven-dimensional hypercube with 84 penteract 5-faces. Under Hurwitz’s automorphisms theorem, a smooth connected Riemann surface 𝑋 of genus 𝑔>1 will contain an automorphism group whose order is classically bound to . 84 is the thirtieth and largest 𝑛 for which the cyclotomic field has class number 1 (or unique factorization), preceding 60 (that is the composite index of 84) and 48. Finally, there are 84 zero divisors in the 16-dimensional Sedenions .
Aut(X)G
|G|≤84(g-1)
Q()
ζ
n
5
27
5
84
5
110
5
133
5
144
5
()
3
3
5
(*3*7)
2
2
5
(2*5*11)
5
(7*19)
5
2
(*3)
2
2
(
1
)Elkies Taxi Cab Formula and its factorization
The Hardy-Ramanujan formula (the original “taxi cab” number) and the equation for the generalized quaternion helps in better understanding of the Leech Lattice which forms a quantum lattice basis for the Higgs Field.
3
9
3
10
3
12
3
1
3
()
2
3
3
(2*5)
3
(*3)
2
2
3
1
(
2
)Hardy-Ramanujan Taxi Cab Formula and its factorization
8 X |
72 6 X |
180 4 X |
144 2 X |
36 0 X |
(
3
)The Generalized Quaternion equation
2
1
2
2
2
3
2
4
2
5
2
6
2
7
2
8
2
9
2
10
2
11
2
12
2
13
2
14
2
15
2
16
2
17
2
18
2
19
2
20
2
21
2
22
2
23
2
24
2
70
(
4
)Prime Sum Gap Formula
Understanding the prime factorization of these formulas and equations gives clues to the nature of underlying information patterns of the zoo of the “elementary particles and forces”. For example, diverse entitles such as the mu neutrino, positron, D± meson, and the internal structure of the nucleons, proton and neutrons, can be explicated. Moreover, the “physical forces” and their relationship to each other clarified precisely with the help of comparing the factorization of the 358 embedded maximal subgroups of the 27 Finite Non-Abelian Sporadic Groups.
Modular Forms of one variable:
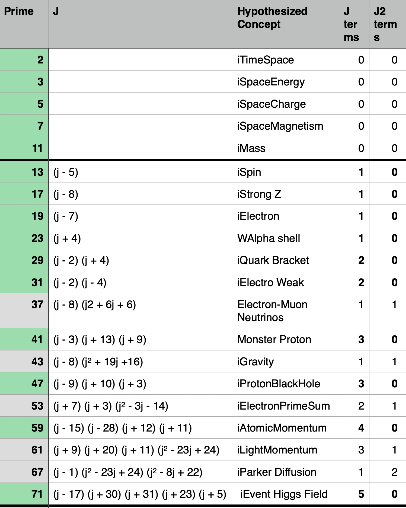
The modular forms of one variable give a unique insight into the internal structure of primes. The 15 SuperSingular Primes, which are the prime factors of the Monster Group can be seen clearly in the following table with a J2 term of 0. In particular, the singular values of the first 20 primes, corresponds with the Sporadic Group Framework, giving insights to physical and information properties of the particle zoo and the cosmic menagerie.
Table 1.
Singular Values of Prime Modular Forms
Epsilon Normed Division Algebras:
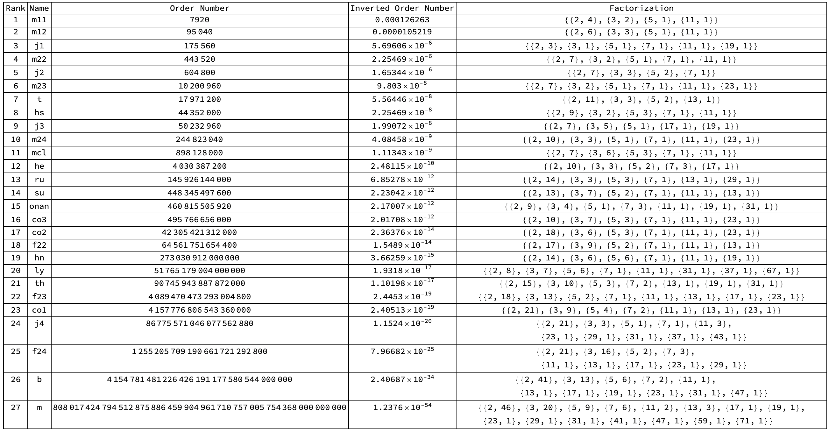
An epsilon normed division algebra A(ϵ) retains many of the structural properties of normed division algebras but with a tolerance for "small" deviations. Moreover, these deviations can contain huge amount of finite information content via the Framework of Finite Simple Groups because epsilon is set at a finite unit 1 fraction embedded within the group order of a Sporadic Group. For example, the Epsilon Normed Division Algebra A(1/7920), is normed by the order number of elements of the Mathieu 11 Finite Simple Group (considered the center of information of the Proton), the first of the 27 Finite Non-Abelian Sporadic Groups. See Appendix Table 2 & 3. One also can use the Monster Group (the “largest” Finite Sporadic Group) as a basis for a A(ϵ) -> A(1/|M|) an underlying finite quantum floor in the form of the Higgs Field. See Appendix Table 2 & 3.
- Relevance: In conventional physical theories, information science is a step child to differential and integral calculus and particularly Lie Algebras. Physicists like Gell-mann and Feynman, excellent in particle physics theories, lead to major insights into particle physics, in their “mathematical hacks” (e.g., Lie group renormalization and Lagrangian vertex algebras). However, they were missing an understanding of Information Science and modular forms, and hence did not have the ability (and knowledge) to incorporate a more finite, discrete, and logic-based understanding of physical phenomena such as: Majorana Zero Modes, neutrino oscillation, Lamb shift, Aharonov-Bohm effect, Jahn-Teller effect, and the Unruh effect.
Connecting the Concepts and Percepts
1. Symmetry in Gestalt Physics: Simple Finite groups and Moufang loops offer ways to understand more nuanced forms of symmetries and asymmetries underlying physical laws. Symmetry principles often dictate the form of physical laws and can reveal why certain constants are the way they are.
1. Symmetry in Gestalt Physics: Simple Finite groups and Moufang loops offer ways to understand more nuanced forms of symmetries and asymmetries underlying physical laws. Symmetry principles often dictate the form of physical laws and can reveal why certain constants are the way they are.
2. Variability and Constants: The potential variability of physical constants in different contexts (e.g., near hypothesized singularities, in high-energy physics) can sometimes be better understood using these mathematical and informational frameworks, which allow for more complex relationships than the information poor Abelian or Non-Abelian algebras and/or Poisson Brackets and Lie Brackets via Lie Algebras via calculus and tensors.
3. Algebraic Information Structures and Physical Theories: Exploring how different algebraic information structures serve a symbiotic relationship in physical theories will lead to new insights into existing physical constants. Epsilon Normed Division Algebras might play a role in a Framework beyond the Standard Model, impacting our understanding of G and c.
Conclusion
The nature of physical constants is a complex interplay of empirical observation and informational mathematical theory (Gestalt Science). Simple finite groups and Moufang loops offer sophisticated sources (Gestalt Mathematics) to explore and understand these constants, especially in extreme or non-classical realms of physics. By examining these information structures, we gain deeper insights into the symmetry and fundamental nature of the universe (Gestalt Physics), uncovering new facets of how physical constants operate and relate to each other in a more integrated and dynamical way.
The nature of physical constants is a complex interplay of empirical observation and informational mathematical theory (Gestalt Science). Simple finite groups and Moufang loops offer sophisticated sources (Gestalt Mathematics) to explore and understand these constants, especially in extreme or non-classical realms of physics. By examining these information structures, we gain deeper insights into the symmetry and fundamental nature of the universe (Gestalt Physics), uncovering new facets of how physical constants operate and relate to each other in a more integrated and dynamical way.
Appendix
Table 2.
27 Finite Non-Abelian Sporadic Simple Groups and the finite rational fraction numbers
Table 3.
27 Finite Non-Abelian Sporadic Simple Groups
References
1
.Modular Functions of One Variable, Lecture notes in mathematics 320, QA 3 L2, no 470, Table 6, SuperSingular Values, pages 143-144.
2
.Keirsey, David, “On the Nature of Time and Clocks” Web Resource. https://www.wolframcloud.com/obj/keirsey/Published/On%20the%20Nature%20of%20Time%20and%20Clocks.nb
Selected Bibliography
1
.The Finite Simple Groups, R.A. Wilson, Graduate Texts in Mathematics 251, Springer, 2009.
2
.The Cosmic Revolutionary’s Handbook, Luke A. Barnes & Geraint F. Lewis, Cambridge University Press, 2020.
3
.Lost in Math, Sabine Hossenfelder, Basic Books, 2018.
4
.On Quaternions and Octonions, John Conway and Derek Smith, A K Peters/CRC Press, 2003.
5
.Symmetry and the Monster, Mark Ronan, Oxford University Press, 2006.