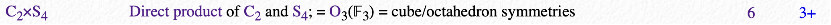Sporadic Epsilon Normed Algebras
Sporadic Epsilon Normed Algebras
David Mark Keirsey
R & D Intelligent Systems
A Special Class of Normed Lattice Algebras are defined for modeling the universe
Epsilon normed algebras can be used to explore transformations of algebras, leading to insights into the robustness in modelling the dynamic physical constants of the universe. Using the 27 Finite Non-Abelian Sporadic Groups as a framework for embedding information into these algebras, they are relevant in theoretical physics, where deviations from exact symmetries open up to exact anti-symmetries, axi-symmetries, gyro-symmetries, and asymmetries of the quantum and cosmic worlds.
Introduction
Introduction
Epsilon normed lattice algebras can be used to explore transformations of algebras, leading to insights into the robustness in modelling the dynamic physical constants of the universe. Using Finite Non-Abelian Sporadic Groups as framework for embedding information into these algebras, they can be relevant in theoretical physics, where deviations from exact symmetries open up to exact anti-symmetries, axi-symmetries, gyro-symmetries, and asymmetries of the quantum and cosmic worlds. In some sense, Epsilon normed lattice algebras are finite rational algebras, a new form of finite, threshold-based Diophantine equations. The concept of iClocks will be introduced to relate to information symmetries/asymmetries.
The current concept of a physical “constant” is too simplistic in the quantum and cosmic realms. The nature of a physical constant, a “quantity,” is also wrapped up with “qualities” in the form of “properties” and/or “factors and ratios.” There are different kinds of numbers (quantities), the standard mathematical number systems are numerous: Cardinal numbers, Ordinal numbers, Whole numbers, Integer numbers, Rational numbers, Algebraic Numbers, Transcendental numbers, Real numbers, Normed Division Algebras (Real: , Complex: , Quaternion: , Octonion: “numbers”), and Clifford Algebras (e.g. Sedenions: ) are the principle examples. Physical qualities, like mass, energy, length, depth, time, spin, charge are in complicated relationships in the realms of the small (quantum) and large (cosmic). Developing a deeper understanding of the incomplete analysis of quantity and quality together, requires complementing them with a more sophisticated informational and computational framework.
“The familiar probability function or functional, and the wave equation, of standard quantum theory provide a mere continuum idealizations and by reason of this circumstance conceal the information-theoretic source from which they derive.” -- John Wheeler
Normed Algebras
Normed Algebras
Following the recipe in John Baez’s paper Octonions , one can define Epsilon Normed Division Algebras, with certain key modifications. The following outlines their construction and properties.
[1]
(page149)
1) Normed Division Algebras:
A normed division algebra is a finite-dimensional algebra 𝐴 over the real numbers with a norm || ⋅ || such that || 𝑥𝑦 || = || 𝑥 || ⋅ || 𝑦 || for all 𝑥,𝑦 ∈ 𝐴. 𝐴 is a division algebra and that || 1 || = 1. An algebra A has multiplicative inverses if for any nonzero α ∈ A there is an element ∈ A with α = α = 1.
-1
α
-1
α
-1
α
Examples of normed division algebras include the real numbers (1 dimension), complex numbers (2 dimensions), quaternions (4 dimensions), and octonions (8 dimensions).
2) Epsilon Normed Algebras:
The concept of an epsilon normed division algebra allows a deviation from the strict normed division algebra properties. An Epsilon Normed Division Algebra is defined as a 4-dimensional normed algebra 𝐴 over the rational numbers.
Specifically, in an epsilon normed division algebra, the norm condition is relaxed but also constrained by any rational epsilon constant (0 < ϵ < 1) such that || 𝑥𝑦 || ≲ (ϵ + 1) || 𝑥 || ⋅ || 𝑦 || for all rationals 𝑥,𝑦 ∈ 𝐴
3) Sporadic Epsilon Normed Algebras:
Even more specifically, in a Sporadic Epsilon Normed Division Algebra, the norm condition || 𝑥y || ≲ (ϵ + 1) || 𝑥 || ⋅ || 𝑦 || is relaxed and constrained by the rational number term constant epsilon where (ϵ = 1/(the order number of a Finite Non-Abelian Sporadic Group))
Construction of Epsilon (Rational) Normed Division Algebras:
Start with the standard normed division algebra but with strictly rational coefficients.
Introduce a perturbation parameter 𝜖 to the multiplication operation so that the norm condition becomes:
|| xy || ≤ (ϵ + 1) || x || ⋅ || y ||
This perturbation allows for the construction of new algebras that maintain division properties up to a small term controlled by 𝜖.
This perturbation allows for the construction of new algebras that maintain division properties up to a small term controlled by 𝜖.
A vector space is a finite-dimensional module over the field of real numbers. An algebra A will be a vector space that is equipped with a bilinear map m: A × A A called `multiplication’ and a nonzero element 1 ∈ A called the `unit’ such that m(1; a) = m(a; 1) = a. Abbreviate m(a; b) as ab. Do not assume the algebras are associative. Given an algebra, the rational numbers as elements of this algebra via the map α α1.
An algebra A is a division algebra if given a; b ∈ A with ab = 0, then either a = 0 or b = 0. Equivalently, A is a division algebra if the operations of left and right multiplication by any nonzero element are invertible. A normed division algebra is an algebra A that is also a normed vector space with || ab || = || a || · || b ||. Thus A is a division algebra and that || 1 || = 1. An algebra A has multiplicative inverses if for any nonzero α ∈ A there is an element ∈ A with α = α = 1. An associative algebra has multiplicative inverses iff it is a division algebra. However, this fails for nonassociative algebras. There are three levels of associativity. An algebra is power-associative if the subalgebra generated by any one element is associative. It is alternative if the subalgebra generated by any two elements is associative. Finally, if the subalgebra generated by any three elements is associative, the algebra is associative. Therefore , , , are associative.
-1
α
-1
α
-1
α
Construct a division algebra A(ϵ) without multiplicative inverses by taking A(ϵ) ⊂ (), the quaternions with strictly rational coefficients, and modifying the product slightly setting = -1 + ϵj for some small nonzero rational number while leaving the rest of the multiplication table unchanged. The element i then has both right and left inverses, but they are not equal. Thus A(ϵ) is a 4 dimensional (finite and rationalized quaternion) epsilon normed division algebra.
2
i
Properties:
An epsilon normed division algebra retains many of the structural properties of normed division algebras but with a tolerance for “small” deviations. Moreover, these deviations can contain huge amount of finite information content via the Framework of Finite Simple Groups because epsilon is set at a finite unit 1 fraction embedded within the group order of a Sporadic Group or the Non-Abelian Finite Lie Simple Group Families. For example, the Epsilon Normed Division Algebra A(1/7920), is normed by the order number of elements of the Mathieu 11 Finite Simple Group, the first of the 27 Finite Non-Abelian Sporadic Groups. See Appendix Table 1.
An epsilon normed division algebra retains many of the structural properties of normed division algebras but with a tolerance for “small” deviations. Moreover, these deviations can contain huge amount of finite information content via the Framework of Finite Simple Groups because epsilon is set at a finite unit 1 fraction embedded within the group order of a Sporadic Group or the Non-Abelian Finite Lie Simple Group Families. For example, the Epsilon Normed Division Algebra A(1/7920), is normed by the order number of elements of the Mathieu 11 Finite Simple Group, the first of the 27 Finite Non-Abelian Sporadic Groups. See Appendix Table 1.
These algebras can be useful in various informational, mathematical, envolutionary (functional evolution), and physical contexts where exact norm preservation is not necessary, but preservation of finite information fields within an epsilon range is sufficient.
The most applicable for exploring the quantum world will be the Sporadic Epsilon Normed Division Algebra (SENDA) that uses the order number of the Monster Group A(1/|M|) which represents the Higgs Field. The value of this SENDA ϵ is ~ 1.2376x, although the value of 1/|M| is an finite and exact rational number serving as an finite “infinitesimal” and covers the first 20 primes including the 15 supersingular prime dimensions 2, 3, 5, 7, 11, 13, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71
-53
10
The most applicable for exploring the quantum and cosmic world will be the Epsilon Normed Division Algebra (ENDA) that uses the order number of the Exceptional E8 Non-Abelian Lie Simple Group A(1/|E8(2)|). The (finite) rational value of this ENDA ϵ is ~ . The prime factors of E8(2) are 2, 3, 5, 7, 11, 13, 17, 19, 31, 41, 43, 73, 127, 151, 241, 331. The prime factors of E7(2) are 2, 3, 5, 7, 11, 13, 17, 19, 31, 43, 73, 127. The prime factors of E6(2) are 2, 3, 5, 7, 13, 17, 31, 73.
2.96029×
-75
10
Epsilon normed division algebras can be used to explore Moufang loop transformations of algebras, leading to insights into their stability and robustness. They can also be relevant in theoretical physics, where deviations from exact symmetries open up to exact anti-symmetries, axi-symmetries, gyro-symmetries, and asymmetries of the quantum and cosmic worlds.
In essence, John Baez’s nascent idea of epsilon normed division algebras opens up a way to study and utilize algebraic structures that are nearly norm-preserving, providing a broader framework that includes Finite rational numbers based normed division algebras as special cases when 𝜖 = 0 and a more nuanced understanding of “di-mens-ions” from an informational perspective.
Group Lattice Algebras and Prime Di-mensions
Group Lattice Algebras and Prime Di-mensions
Di- Greek: containing two, mēnsiōn Latin: measuring.
Ever since, Hermann Grassmann introduced his nascent ideas in 1844, about linear algebra, vectors, and k-dimensions there has been serious work on this general notion of “di-mensions.” According to Wolfram’s Mathworld, these include numerous concepts such as: Capacity Dimension, Codimension, Correlation Dimension, Exterior Dimension, Four-Dimensional Geometry, Fractal Dimension, Hausdorff Dimension, Kaplan-Yorke Dimension, Krull Dimension, Lebesgue Covering Dimension, Lyapunov Dimension, Poset Dimension, q-Dimension, Similarity Dimension, Vector Basis.
Diophantine Algebras, Group Prime Dimensions, Group Prime Sum Dimensions
Besides the numerical kinds of dimensions defined by mathematicians, information dimensions can be characterized as in Diophantine Algebras, which Epsilon Normed Algebras are special examples. Diophantine algebra refers to the algebraic structures and techniques used to analyze Diophantine equations, which are polynomial equations where solutions are sought in integers or rational numbers. Epsilon Normed Algebras are both finite in a regular “dimensions,” i.e., four dimensions, and finite in “magnitude.” Where the finiteness of the magnitude is determined by the prime factors as the thresholds [limits] or information and numerical boundaries: in other words, “group information dimensions.” There are two kinds of group dimensions: group prime factor dimensions and group prime sum dimensions.
Group Prime Dimensions
One way to think of Group Prime dimensions could be within the context of vector spaces or algebraic structures that have dimensions based on a finite set of prime numbers. In linear algebra, a vector space can have a dimension that is a prime number, which have certain properties of the space, such as factorization and decomposability of elements. As example, the smallest integer Sporadic Group M11 which has the group order of 7920 elements and a prime factorization of **5*11 = 16*9*5*11 = 7920. Because M11 is a Simple group, it is an information atom: where rational numbers 1/-7920, 0/-7920, 0/7920, 1/7920 represent the extent of the atomic group information. M11, which represents the information atom iProton/iAnti-Proton, has also more internal structure and process. M11 has maximal subgroups 2S4 (48 elements), S5 (120 elements), M9:2 (144 elements), L2(11) (660 elements) M10 (720 elements). Internal to the M11 information atom, the maximal subgroup groups represent different information quanta. As one example the first conjugacy maximal subgroup of M11, 2S4 group represents the cube/octahedron symmetries, and physically the information quanta of the plus charge of the iProton/iAnti-Proton (whereas 1/-48 represents the negative charge of Anti-Proton).
4
2
2
3
Another kind of information analysis involves Group Prime-Sum dimensions which have decomposition properties for groups, rings, or other algebraic structures. A geometric object or space could be constructed where its dimensionality is expressed as a sum of primes. Continuing the example of M11, the iProton, the sum of prime factors is 16+9+5+11=41. The Higgs Field, represented in the Monster Group, is the only Sporadic Group which has 41 as a prime factor. Finite Partition theory and Non-Abelian Simple Groups are related to nature of the quantum and cosmic worlds.
A better understanding of the structure and process of the quantum world can be done using the Group Prime information dimensions and Group Prime-Sum information dimensions integrated by the 27 Sporadic Group Framework. The integration is accomplished by using the Monster Group as an information infimum in the Framework and a Sporadic Epsilon Normed Algebra, e.g. A(1/|M|).
Group Lattice Algebras
On the other hand, using Group Lattice Algebras integrating the Sporadic Group Framework and the 17 Finite Non-Abelian Lie Simple Group families both the quantum world and the cosmic world can be better understood. Lattice Algebras can represent the symmetries/asymmetries of partially ordered sets.
In mathematics, the infimum (abbreviated inf; pl.: infima) of a subset S of a partially ordered set P is the greatest element in P that is less than or equal to each element of S if such an element exists. If the infimum of S exists, it is unique, and if b is a lower bound of S then b is less than or equal to the infimum of S. Consequently, the term greatest lower bound (abbreviated as GLB) is also commonly used. The supremum (abbreviated sup; pl.: suprema) of a subset S of a partially ordered set P is the least element in P that is greater than or equal to each element of S, if such an element exists. If the supremum of S exists, it is unique, and if b is an upper bound of S, then the supremum of S is less than or equal to b. Consequently, the supremum is also referred to as the least upper bound (or LUB).
Epsilon Normed algebras opens up a way to study and utilize algebraic structures that are nearly norm-preserving, providing a broader information framework. The Sporadic Group as Simple Groups provides a framework of generalizing the Epsilon Normed algebras to Epsilon Group Lattice Normed algebras with two parameters ϵ and λ to create both an infimum ϵ and a supremum λ.
Information Group Lattice Normed algebras
Similar to Epsilon Normed algebras, Information Group Lattice Normed algebras IGLNA(inf:ϵ,sup:λ) are defined as a Normed Rational algebra bracketed by a Simple Group, , limited by supremum value λ = 1/|| and a Simple Group, , limited by infimum value ϵ = 1/(||*||), such that || < ||. As an example, EGLNA(ϵ=1/(|M11|*|M12|), λ=1/|M11|) as a Information Group Lattice Normed algebra includes 55 maximal subgroups of the Sporadic Group Framework plus the two Simple Groups M11 and M12 (information Neutron) and M11 (information Proton).
G
1
G
1
G
2
G
1
G
2
G
1
G
2
The construction of the Information Normed algebra is as follows.
Construct a division algebra IA(ϵ, λ) without multiplicative inverses by taking IA(ϵ, λ) ⊂ (), the quaternions with strictly rational coefficients, and modifying the product, setting = -1 + ϵj and = -1 + λk for some small nonzero rational numbers ϵ and λ, such that 1 > λ > ϵ > 0 while leaving the rest of the multiplication table unchanged. The elements i and j and k then have right and left inverses, but they are not equal. Thus IA(ϵ, λ) is a 4 dimensional (finite and rationalized quaternion) normed algebra.
2
i
2
j
Simple Groups and Prime Singular Values
Simple Groups and Prime Singular Values
Simple groups have no nontrivial normal subgroups other than the identity A2 (the trivial group) and the group itself. They play a critical role in understanding the concepts and percepts of: symmetry, antisymmetry, axi-symmetry, gyro-symmetry, and asymmetry.
Finite simple groups play a crucial role in understanding the structure of all finite groups. Any finite group can be decomposed into a series of normal subgroups, where each quotient is a simple group. Hence, finite simple groups can be thought of as the fundamental building blocks of finite groups and fundamental building blocks of “information atoms (aka, finite quanta structure process)” and “information forces (aka, finite qualia process structure).”
The Finite Non-Abelian Simple groups are special in that they can serve as information quanta, information atoms, information molecules, and information forces. The infinite family of primes are in the form "information quanta" of Finite Abelian Simple Groups. The 16 Finite Non-Abelian Lie Simple Families of groups can represent physical and informational concepts of both a precise quantity and several precise qualities in precise ratios. Finally, and most importantly from an informational point of view, the 27 Finite Sporadic Simple Groups (Unique, Non-Abelian) and their 358 maximal subgroups, form a Finite Total Preorder Framework. Moreover, the 15 SuperSingular Primes form a partial ordered lattice Preorder Framework to model the universe and its processes.
The 27 Sporadic Groups and their immediate maximal subgroup relations
Over arching all groups, are Moufang loops. A Moufang loop is a quasigroup (a set with a binary operation) that satisfies the Moufang identities. All groups are Moufang Loops.
Unlike groups, Moufang loops do not necessarily obey the associative law but maintain a weaker form of associativity through the Moufang identities: bi-associativity (a looser notion of connectivity). In some sense, Abelian and Non-Abelian Moufang Loops encompass a more informational form of a group, where the "identity element" is "fluid" within the Loop. Moreover, Non-Abelian Moufang Loops, having their left and right Bol loops that can combine to form, finitely, into open information connections of either peak or valley information gaps (up and down finite cusps of mixed (e.g., entangled) or orthogonal physical qualities). These finite information cusps can act like Weyl liquid surface manifold quanta or Ricci gas balloon manifold quanta.
Modular Forms of one variable:
The modular forms of one variable give a unique insight into the internal structure of primes. The 15 SuperSingular Primes, which are the prime factors of the Monster Group can be seen clearly in the following table with a J2 term of 0. In particular, the singular values of the first 20 primes, corresponds with the Sporadic Group Framework, giving insights to physical and information properties of the particle zoo and the cosmic menagerie. See Table 1 in the appendix.
The modular forms of one variable give a unique insight into the internal structure of primes. The 15 SuperSingular Primes, which are the prime factors of the Monster Group can be seen clearly in the following table with a J2 term of 0. In particular, the singular values of the first 20 primes, corresponds with the Sporadic Group Framework, giving insights to physical and information properties of the particle zoo and the cosmic menagerie. See Table 1 in the appendix.
The Simple Family Groups
Understanding the symmetries and asymmetries in particle physics, the field extensions beyond the Standard Model are enhanced by correspondences drawn from the Supersingular prime values associated with 27 Simple Sporadic groups and the 17 Simple group families. The 17 Finite Simple Group Families serve as information bases and constraints for star systems, neutron stars, and black holes.
The 17 Finite Simple Families of groups can be viewed as either embedding, intersecting, or being embedded into the Sporadic Group Framework. See Table 4 for the 17 Finite Simple Families.
The largest simple group family the Exceptional Chevalley E8(q) where q is a prime number, in some sense, embeds all the Simple Families and the Sporadic Groups. The three Chevalley Exceptional Lie Groups embed each other. E8 embeds E7. E7 embeds E6. It is posited that E8 family of Simple Groups are intimately involved with the Black Hole dynamics. It is posited that the second largest simple group family E7(q) are intimately involved with Neutron Star dynamics. It is posited that the third largest simple group family E6(q) are intimately involved with Star dynamics. All other Finite Lie Simple Families are involved (in some sense “entangled”) with both the cosmic dynamics and quantum dynamics, having some of the finite groups being embedded in the maximal subgroups of the Sporadic Framework.
Maximal Subgroup Strata
The embedded groups within the Framework essentially form information strata (“group layers”) that make a more complicated set of relationships of informational physical entities and informational physical forces interweaving the quarks, leptons, mesons, and baryons. However, even though the relationships are more complicated in the Framework’s perspective, they are more understandable. In contrast, the Standard Model is semantically incomplete, hence not as understandable from a first principles point of view. In other words, Heisenberg’s uncertainty principle and Pauli’s exclusion principle do not explain enough in detail to understand how the quantum world works.
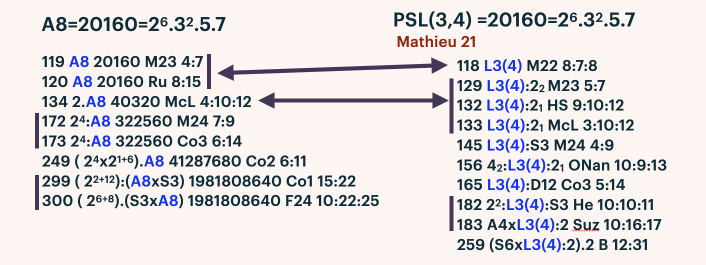
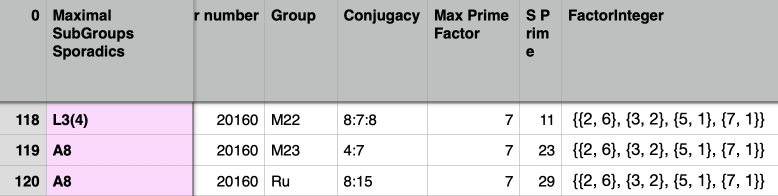
For example, from the Framework perspective, , serve as maximal subgroups or part of maximal subgroups of some of the Sporadic Groups. As it turns out, the Alternating Group with group element order number of 8!/2 is involved in 8 maximal subgroups of 8 Sporadic Groups. And the Projective Linear Group PSL(3,4): also known as the Mathieu 21 group, is involved in 10 maximal subgroups of 10 Sporadic Groups. and PSL(3,4) are different groups but have the same order number, i.e., both have 20160 group elements.
sometheAlternatingGroupfamily,
A
n
A
8
A
8
A8 and PSL(3,4) Finite Simple Non-Abelian Lie Groups as maximal subgroups of the Sporadic Framework
A8, Alternating Group, a maximal subgroup of Mathieu 23 and Rudvalis Simple Sporadic Groups.
Maximal Subgroups of Order Number |S8|: the Symmetric Group of 8!, 2.A8, PSL(3,4):2, 2^4:A7
A7, Alternating Group: two maximal subgroups of Mathieu 22 and ONan, one maximal subgroup of Suzuki.
Sheldon Glashow, along with Howard Georgi, proposed the SU(5) Grand Unified Theory (GUT) in 1974. This theory aimed to unify the Standard Model {U(1)xSU(2)xSU(3)}: the electromagnetism U(1), weak SU(2), and strong force SU(3), under a single gauge group, SU(5). The GUT theories were not confirmed and pretty much ruled out by the experiments of the LHC. The problem with gauge fields is they assume that renormalization parameters of the Standard Model are sufficient to characterize the gauges. The renormalization parameters are ad-hoc and no justification other them being measured as statistical values.
One can think of these Simple Groups as “standing waves” or wave packets (finite in time duration) at a certain frequency, that is, an information time Clock: itClock.
Schrödinger’s initial model of De Broglie’s matter waves.
Finite Rational Limits: iClocks
The nature of physical entities and processes are more complex in the context of kinematic and inertial forms of time and clocks. The information relationships between physical entities and processes in terms of time, clocks, energy, mass, and space can be seen more clearly with understanding the nature of "information binds and leaks." The general concept to capture this nature will be named: iClocks: information clocks, representing a group G of rational value of 1/(x/y), where the group order number would be x*y.
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its essential (irreducible representation) network structure. The set of all automorphisms of an object forms a group, called the automorphism group. It is, loosely speaking, the symmetry group of the object. For Finite Simple Groups, the symmetries/asymmetries are directly visible via their maximal subgroups and prime indexes because Finite Simple Groups and their information embedded maximal subgroups are in some sense information atoms that correspond to physical entities and/or physical processes. These physical entities can have several information symmetric/asymmetrical properties like space, length, mass, mv-momentum, p-momentum, charge, spin, energy, information duration, and information boundaries.
Finite Simple groups play a critical role in understanding the concepts and percepts of: symmetry, antisymmetry, axi-symmetry, gyro-symmetry, and asymmetry. Finite Simple Groups can be seen as “time knots,” as they are “information atoms.” Groups, in general, can be seen as “time windings.” In addition, Non-Abelian Finite Simple groups can be seen as containing “internal time clocks” which are special collection of subgroups. Moreover, there are a set of special subgroups embedded in the Simple Group called “maximal subgroups” just below the group itself: “information bubbles” just below the entities “surface”. Every maximal subgroup (MS) has a positive integer prime index (px) of a Simple Group G such that |G| = |MS|*px.
Besides “internal time clocks” one can also start to talk about internal information clocks, or iClocks. An iClock can be integer value or even a rational value, but representing a physical quality or physical ratio.
Hamilton denoted the versor of a quaternion q by the symbol U q. He was then able to display the general quaternion in polar coordinate form q = T q U q, where T q is the norm of q. The norm of a versor is always equal to one; hence they occupy the unit 3-sphere in ℍ. Examples of versors include the eight elements of the quaternion group. Of particular importance are the right versors, which have angle 90 degrees. These versors have zero scalar part, and so are vectors of length one (unit vectors). The right versors form a sphere of square roots of −1 in the quaternion algebra. The generators i, j, and k are examples of right versors, as well as their additive inverses. Other versors include the 24 Hurwitz quaternions that have the norm 1 and form vertices of a 24-cell polychoron.
Diophantine Formulas and Equations
Understanding the prime factorization of Diophantine formulas and equations gives clues to the nature of underlying information patterns of the zoo of the “elementary particles and forces”. Diophantine equations, which are polynomial equations where solutions are sought in integers or rational numbers.
Prime Sum Gap Formula
The Generalized Quaternion equation
First Diophantine Triangular Harmonic Formula
Simple Group Information Gauged Algebras
It should be noted that there are 16 boolean operators of Boolean logic.
The Hardy-Ramanujan formula (the original “taxi cab” number) and the equation for the generalized quaternion helps in better understanding of the Leech Lattice which forms a quantum lattice basis for the Higgs Field. There several key formula that hint at the relationship between the structure of the prime numbers and physical entities and forces.
Hardy-Ramanujan Taxi Cab Formula and its factorization
Elkies Taxi Cab Formula and its factorization
84 Sedenion Zero Divisors
Conclusion
Conclusion
Epsilon-normed lattice algebras offer a way to examine transformations within algebras, providing insights into the robustness of models for the universe's dynamic physical constants and physical forces. By using Finite Non-Abelian Sporadic groups as a framework to embed information into these algebras, they become applicable in theoretical physics. Here, deviations from exact symmetries allow for exact anti-symmetries, axi-symmetries, gyro-symmetries, and asymmetries within quantum and cosmic realms. In essence, epsilon-normed lattice algebras function as finite rational algebras, resembling a novel form of finite, threshold-based Diophantine equations. Additionally, the concept of iClocks was introduced to connect with information symmetries and asymmetries of the universe’s dynamic physical waveforms and forces.
Appendix
The Finite Non-Abelian Simple groups are special in that they can serve as information quanta, information atoms, information molecules, and information forces. The 17 Non-Abelian Lie Simple Family of groups can represent physical and informational concepts of both a precise quantity and several precise qualities in precise ratios. Finally, and most importantly from an informational point of view, the 27 Finite Sporadic Simple Groups (Unique, Non-Abelian) and their 358 maximal subgroups, form a Finite Total Preorder Framework. Moreover, the 15 SuperSingular Primes form a partial ordered lattice Preorder Framework to model the universe and its processes. This Framework has no parameters to it: there are no ad-hoc fudge factors to over fit the data, unlike String Theory which have an infinite set of ad-hoc parameters to choose from.
References
1
.Baez, John, “Octonions,” BULLETIN (New Series) OF THE AMERICAN MATHEMATICAL SOCIETY, Volume 39, Number 2, Pages 145-205
S 0273-0979(01)00934-X
Article electronically published on December 21, 2001
S 0273-0979(01)00934-X
Article electronically published on December 21, 2001
2
.Keirsey, David, “The Nature of Physical Constants” Web Resource. https://www.wolframcloud.com/obj/keirsey/Published/Ontology%20of%20Physical%20Constants.nb.
3
.Keirsey, David, “On the Nature of Time and Clocks” Web Resource. https://www.wolframcloud.com/obj/keirsey/Published/On%20the%20Nature%20of%20Time%20and%20Clocks.nb
4
.Modular Functions of One Variable, Lecture notes in mathematics 320, QA 3 L2, no 470, Table 6, SuperSingular Values, pages 143-144.