Exploring Correlation in Statistics
Exploring Correlation in Statistics
Correlation is a measure of the strength of a linear relationship between two numerical variables.
Why do we care about correlation?
Why do we care about correlation?
Correlation is important in Statistics because it allows us to quantify the relationship between quantities. For example, you probably have wondered if there’s a relationship between things like the amount of calories you consume and your weight, number of fast-food restaurants in a neighborhood and obesity rates, income and mortality rates, etc. The strength of a linear relationship between quantities like these ones is measured using the linear correlation coefficient. When, we say two variables are correlated, we are saying that the variables seem to have a strong relationship between each other, but be careful, correlation does imply causation.
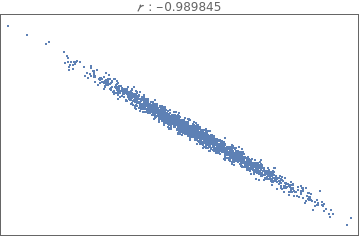
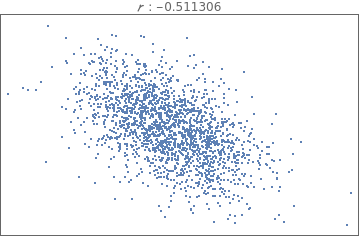
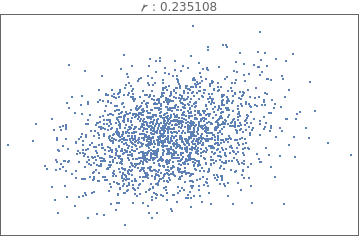
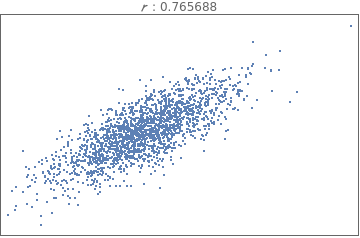
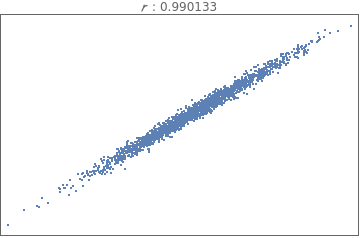
The correlation coefficient measures the strength of a linear relationship between two paired numerical variables, and it describes the direction (positive or negative) and strength of a relationship between two variables (how well data fit a straight-line patter).
With the help of the Wolfram language and data from the Wolfram repository, we will be able to do an overview of how to calculate and interpret the correlation coefficient .
The correlation coefficient measures the strength of a linear relationship between two paired numerical variables, and it describes the direction (positive or negative) and strength of a relationship between two variables (how well data fit a straight-line patter).
With the help of the Wolfram language and data from the Wolfram repository, we will be able to do an overview of how to calculate and interpret the correlation coefficient .
Correlation Coefficient Properties
only measures the strength of a linear relationship. There may be nonlinear relationships.
is always between -1 and 1 inclusive. -1 means perfect negative linear correlation and +1 means perfect positive linear correlation
has the same sign as the slope of the regression (best fit) line
does not change if the independent (x) and dependent (y) variables are interchanged
does not change if the scale on either variable is changed. You may multiply, divide, add, or subtract a value to/from all the x-values or y-values without changing the value of r.
has a Student’s t distribution
only measures the strength of a linear relationship. There may be nonlinear relationships.
is always between -1 and 1 inclusive. -1 means perfect negative linear correlation and +1 means perfect positive linear correlation
has the same sign as the slope of the regression (best fit) line
does not change if the independent (x) and dependent (y) variables are interchanged
does not change if the scale on either variable is changed. You may multiply, divide, add, or subtract a value to/from all the x-values or y-values without changing the value of r.
has a Student’s t distribution
Comparing and interpreting linear strength relationships from scatter plots
Comparing and interpreting linear strength relationships from scatter plots
In[18]:=
data=BlockRandom[SeedRandom[1];Table[RandomVariate[BinormalDistribution[i],2000],{i,{-.99,-.75,-.25,-.5,0.,.25,.5,.75,.99}}]];
In[19]:=
Grid[Partition[Table[ListPlot[i,PlotStyleDirective[PointSize[Tiny]],FrameTicksNone,FrameTrue,AxesNone,PlotLabelRow[{" : ",Correlation[i][[1,2]]}]],{i,data}],3]]
Out[19]=
The data below shows the before and after weight of young women undergoing anorexia treatment. When you look at the data, what kind of questions might you ask?
◼
Obtain data from Wolfram Repository: Before and after weight of young women undergoing anorexia treatment.
In[110]:=
data=ResourceData["Sample Data: Anorexia Treatment"]
Out[110]=
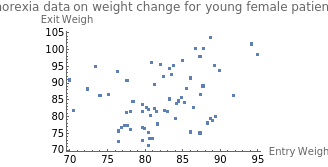
By simply looking at data in a table, it can be difficult to observe whether or not there is a linear relationship between the entry weight and exit weight of the young female patients. A scatter diagram can help us to visualize the distribution of the data.
In[111]:=
ListPlot[data[All,{"EntryWeight","ExitWeight"}],PlotLabel"Anorexia data on weight change for young female patients",AxesLabel{"Entry Weight","Exit Weigh"}]
Out[111]=
By looking at the scatter plot, would you say there is a correlation between the entry and exit weight of the young female patients? The data is widely scattered, and by visual inspection we can observe there doesn’t seem to be a strong correlation between these two variables, but to be sure, let’s calculate the value of .
◼
Calculate
In[112]:=
Correlation[Normal@data[All,"EntryWeight"],Normal@data[All,"ExitWeight"]]
Out[112]=
0.332406
Checking for Linear Correlation
We found the value of the linear correlation coefficient, =0.332406, but what does it mean? To interpret it’s meaning, we can use our knowledge on hypothesis tests and p-values. (* indicates that there is a weak linear relationship between the entry and exit weights, and we can conclude that the weights of the patients are random and there is no evidence to support that the anorexia treatments is effective.*)
(*In cases where we find a strong linear correlation, we can proceed a hypothesis test and find the line best-fit.*)
To interpret the we refer to the computed p-value, if it is less that or equal to the significance level, we conclude there is a linear correlation
Hypothesis Test using p-value from a a t -Test
Hypothesis Test using p-value from a a t -Test
Using the previous example, we can conduct a formal hypothesis test of the claim that there is linear correlation between the entry and exit weights.
To claim that there is linear correlation implies that the linear correlation coefficient is not zero.
:ρ=0 There is no linear correlation
:ρ≠0 There is linear correlation
(*In cases where we find a strong linear correlation, we can proceed a hypothesis test and find the line best-fit.*)
To claim that there is linear correlation implies that the linear correlation coefficient is not zero.
H
o
H
1
(*In cases where we find a strong linear correlation, we can proceed a hypothesis test and find the line best-fit.*)
◼
Plotting the data points and the regression line
In[165]:=
model["ParameterConfidenceIntervalTable"]
Out[165]=
Estimate | Standard Error | Confidence Interval | |
1 | 42.7006 | 14.4311 | {13.9186,71.4826} |
x | 0.51538 | 0.174777 | {0.166799,0.863962} |
Coefficient of Variation 2- Explained Variation
Coefficient of Variation - Explained Variation
2
In cases where we conclude there is a linear correlation between the two variables, we can find a linear equation that expresses y in terms of x (linear regression). The value of is the proportion of the variation in y that is explained by the linear relationship between the two variables.
2
In[127]:=
model["RSquared"]
Out[127]=
0.110494
What does it mean to say there is a positively or negatively linear relationship between two variables?
Practice QuestionsUsing the Wolfram repository, choose a set of data and create your own notebook to do the following: 1. Load data 2. Create a scatter plot 3. based on the scatter plot, provide an estimation for the value of the correlation coefficient between the two variables and explain your answer. 4. Compute the value of the correlation coefficient
Practice QuestionsUsing the Wolfram repository, choose a set of data and create your own notebook to do the following: 1. Load data 2. Create a scatter plot 3. based on the scatter plot, provide an estimation for the value of the correlation coefficient between the two variables and explain your answer. 4. Compute the value of the correlation coefficient
*Hypothesis Test for Correlation
Further Explorations
*Multivariate Correlation
*Nonlinear regression
*Nonlinear regression
Authorship information
Silvani Vejar
06/210/2017
e.vejar@northeastern.edu