You are using a browser not supported by the Wolfram Cloud
Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.
I understand and wish to continue anyway »
WOLFRAM NOTEBOOK
Fourier Series
Fourier Series
The Fourier Series is a representation of a function as an infinite sum of sinusoids.
The Fourier Series
The Fourier Series
History
History
Jean-Baptiste Joseph Fourier introduced the Fourier Series as a way of solving the heat equation in a metal plate. In turn, he concluded that any arbitrary continuous function can be represented by a trigonometric series based on the set of Sin(n·x) and Cos(n·x) functions. In general, the techniques are quite useful when applied to differential equations involving eigen-solutions that are sinusoids.
Motivation
Motivation
Consider a function that does not have a closed form integral formula (i.e. cannot be expressed without using numeric methods):
◼
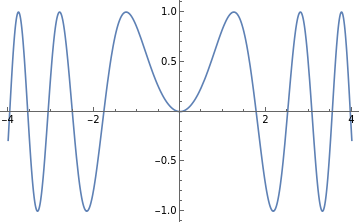
Plot said function: Sin()
2
x
In[16]:=
Plot[Sin[x^2],{x,-4,4}]
Out[16]=
We attempt to the take the integral...
◼
Integrate the function:
In[17]:=
Integrate[Sin[x^2],x]
Out[17]=
π
2
2
π
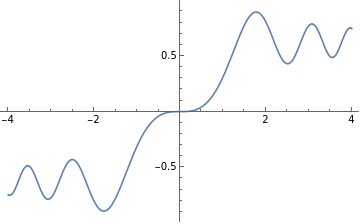
and we can plot the function numerically -
◼
Plot the integral formula:
In[18]:=
Plot[%,{x,-4,4}]
Out[18]=
However there does not exist a closed form solution to such an integral equation.
Theory
Theory
We can define a series of sinusoids that converge to the original function, with the correct constants.
◼
Find the first coefficient in the Fourier Series:
In[78]:=
FourierCoefficient[Sin[x^2],x,1]
Out[78]=
-Erf(1-2π)-Erf(1+2π)-Erfi(-1-2π)+Erfi(-1+2π)
1
8
π
1/4
(-1)
-
4
2
1
2
1/4
(-1)
1
2
1/4
(-1)
1
2
1/4
(-1)
1
2
1/4
(-1)
◼
Express it numerically:
In[79]:=
N[%]
Out[79]=
0.096227-1.38778×
-17
10
◼
Create a list of the first 3 coefficients in the series:
In[80]:=
Table[FourierCoefficient[Sin[x^2],x,i],{i,1,3}]
Out[80]=
-Erf(1-2π)-Erf(1+2π)-Erfi(-1-2π)+Erfi(-1+2π),-Erf(1-π)-Erf(1+π)+Erfi(-1+π)+Erfi(1+π),-Erf(3-2π)-Erf(3+2π)-Erfi(-3-2π)+Erfi(-3+2π)
1
8
π
1/4
(-1)
-
4
2
1
2
1/4
(-1)
1
2
1/4
(-1)
1
2
1/4
(-1)
1
2
1/4
(-1)
1
8
π
1/4
(-1)
-
2
1/4
(-1)
1/4
(-1)
1/4
(-1)
1/4
(-1)
1
8
π
1/4
(-1)
-
9
4
9
2
1
2
1/4
(-1)
1
2
1/4
(-1)
1
2
1/4
(-1)
1
2
1/4
(-1)
In[81]:=
N[%]
Out[81]=
{0.096227-1.38778×,-0.00837573+6.48353×,-0.340173+2.77556×}
-17
10
-17
10
-17
10
We attach these constants to the corresponding functions and obtain an approximation.
◼
Create the 1st order Fourier Series of the function:
In[82]:=
FourierSeries[Sin[x^2],x,1]
Out[82]=
-Erf(1-2π)-Erf(1+2π)-Erfi(-1-2π)+Erfi(-1+2π)-Erf(1-2π)-Erf(1+2π)-Erfi(1-2π)+Erfi(1+2π)+
1
8
π
1/4
(-1)
-+x
4
2
1
2
1/4
(-1)
1
2
1/4
(-1)
1
2
1/4
(-1)
1
2
1/4
(-1)
1
8
π
1/4
(-1)
--x
4
2
1
2
1/4
(-1)
1
2
1/4
(-1)
1
2
1/4
(-1)
1
2
1/4
(-1)
FresnelS[
2π
]2π
◼
Create the 3rd order Fourier Series of the function:
In[3]:=
fourierSeries3=FourierSeries[Sin[x^2],x,3]//N
Out[3]=
0.245943+(0.0932356+0.0238069)+(0.0932356+0.0238069)-(0.00452542+0.00704793)-(0.00452542+0.00704793)+(0.213688-0.264679)+(0.213688-0.264679)
(0.-0.25)-(0.+1.)x
2.71828
(0.-0.25)+(0.+1.)x
2.71828
(0.-1.)-(0.+2.)x
2.71828
(0.-1.)+(0.+2.)x
2.71828
(0.-2.25)-(0.+3.)x
2.71828
(0.-2.25)+(0.+3.)x
2.71828
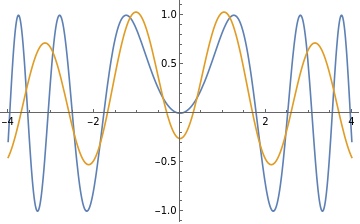
and we can plot said function with Sin() to compare.
2
x
◼
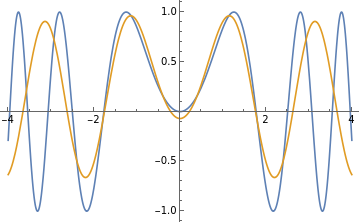
Plot Sin() and our Fourier Series approximation on the same graph:
2
x
In[4]:=
Plot[{Sin[x^2],fourierSeries3},{x,-4,4},PlotLegends"Expressions"]
Out[4]=
Mathematical Exploration
Mathematical Exploration
While we can see that the functions do not overlap exactly, we will explore the convergence of the series.
◼
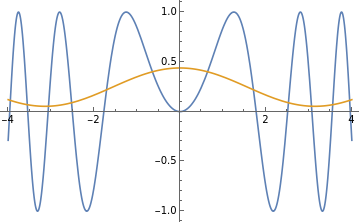
Create the 1st order Fourier Series approximation:
In[11]:=
fourierSeries1=N[FourierSeries[Sin[x^2],x,1]];
◼
and plot:
In[12]:=
Plot[{Sin[x^2],fourierSeries1},{x,-4,4},PlotLegends"Expressions"]
Out[12]=
◼
Create the 4th order Fourier Series approximation:
In[13]:=
fourierSeries4=N[FourierSeries[Sin[x^2],x,4]];
◼
and plot:
In[14]:=
Plot[{Sin[x^2],fourierSeries4},{x,-4,4},PlotLegends"Expressions"]
Out[14]=
◼
Create the 7th order Fourier Series approximation:
◼
and plot:
Application: Numerical Analysis
Application: Numerical Analysis
We can then compare the numerical integral to the integral of the Fourier Series (of which all the terms are integrable).
◼
Compute a list of differences between the integrals as the order of the series increases and plot:
and we can see that the difference is tending towards 0. Thus taking the integral of the Fourier Series of a function is one way to approximate the area under a curve.
Another Application: Solving Differential Equations
Another Application: Solving Differential Equations
Consider the differential equation: y’’ = - kx, k > 0 with boundary condition y(0) = 0, y’(0) = 0.
We will solve this using Fourier series.
We will solve this using Fourier series.
◼
First find the Fourier Series of the right-hand side of the equation.
We show the first few terms here:
We show the first few terms here:
◼
To begin, we compute the second derivative on the left-hand side of the equation for each term:
◼
We then solve for the unknown coefficients, after generalizing the coefficients on the right-hand side.
For the even terms:
For the even terms:
◼
For the odd terms:
◼
Sum up the terms, set k = 1, and plot the solution:
Further Explorations
Explore the Taylor Series Expansion of a Function
Explore Other Sets of Basis Functions That Can Approximate a Function
Authorship information
Michael Dobbs
21.06.17
dobbsm@sonoma.edu