Insert
Sample

Ramsey’s Theorem

Ramsey’s theorem states that for any complete graph, there exists some number such that any edge 2-coloring yields a complete subgraph of that size in one of the colors, or informally, “complete disorder is impossible.”

Friends and Strangers

We begin by looking a famous special case of Ramsey’s theorem, the theorem on friends and strangers, which states that in a group of six people, either three people mutually know each other, or three people mutually do not know each other.
◼
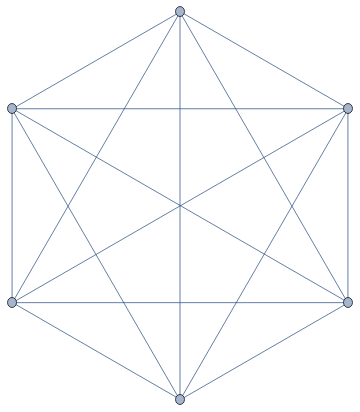
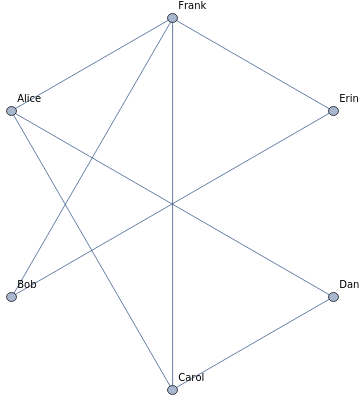
Make a complete graph with 6 vertices
In[1]:=
CompleteGraph[6]
Out[1]=
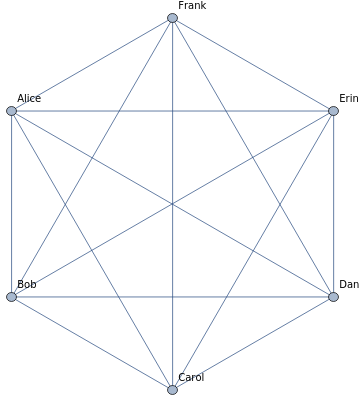
The theorem begins with six people at a party, so we label each vertex to represent person.
◼
Label vertices on the graph
In[2]:=
CompleteGraph[6,VertexLabels{1Alice,2Bob,3Carol,4Dan,5Erin,6Frank}]
Out[2]=
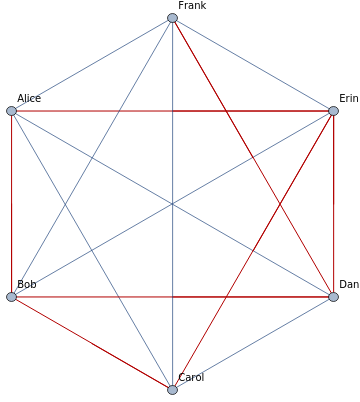
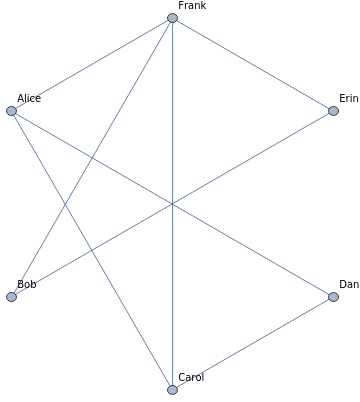
Now assume these people are either mutually friends or strangers. We can use two colors to represent the relations.
◼
Color edges on the graph
In[3]:=
HighlightGraph[CompleteGraph[6,VertexLabels{1Alice,2Bob,3Carol,4Dan,5Erin,6Frank}],{12,15,23,24,35,45,46}]
Out[3]=
A blue edge means two people are friends while a red edge means they are strangers. Now let us separate the two graphs.
◼
Draw the subgraph with only the red edges
In[4]:=
Graph[{12,15,23,24,35,45,46},VertexLabels{1Alice,2Bob,3Carol,4Dan,5Erin,6Frank},EdgeStyleRed]​​
Out[4]=
◼
Draw the complete graph with the red edges removed
In[5]:=
EdgeDelete[CompleteGraph[6,VertexLabels->{1Alice,2Bob,3Carol,4Dan,5Erin,6Frank}],{12,15,23,24,35,45,46}]
Out[5]=
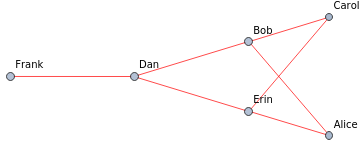
We first check the red subgraph for complete subgraphs with 3 vertices.
◼
Find any cliques of at least 3 vertices in the red subgraph
In[6]:=
FindClique[Graph[{12,15,23,24,35,45,46}],{3,6}]
Out[6]=
{}
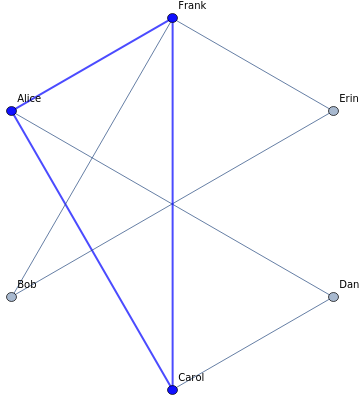
The theorem on friends and strangers tells us that since the red subgraph has no complete subgraphs of size 3, then the blue subgraph must.
◼
Find any cliques of at least 3 vertices in the blue subgraph
In[7]:=
FindClique[EdgeDelete[CompleteGraph[6],{12,15,23,24,35,45,46}],{3,6}]
Out[7]=
{{1,3,6}}
◼
Highlight the clique with thick edges
In[8]:=
HighlightGraph
,StyleSubgraph
,FindClique[EdgeDelete[CompleteGraph[6],{12,15,23,24,35,45,46}],{3,6}],{Blue,Thick}
Out[8]=
◼
Display the 2-colored complete graph and highlight the clique with thick edges
We can try some more examples. Since any 2-coloring will work, we can randomly select an edge set from the graph to represent the other color.
◼
Choose a random edge subset from the complete graph
◼
Display the 2-colored complete graph and highlight cliques of either color with thick edges
◼
Define a function to display the 2-colored complete graph and highlight cliques of either color with thick edges
◼
Apply the function to thirty random edge subsets

Ramsey Numbers

But what happens if we use a complete graph of 5 vertices instead of 6?
◼
Define a function that draws the 2-colored complete graph of 5 vertices whenever there is no clique of at least 3 vertices in either color
We can do an exhaustive search on all possible 2-colorings.
◼
Apply the function to all edge subsets of the complete graph of 5 vertices
So we have a total of 12 counterexamples when the complete graph has only 5 vertices. We can modify the function and run the same exhaustive check on complete graphs of 6 vertices.
◼
Define a function that draws the 2-colored complete graph of 6 vertices whenever there is no clique of at least 3 vertices in either color
◼
Apply the function to all edge subsets of the complete graph of 6 vertices
Since the result set is empty, this proves the theorem on friends and strangers, which we can restate as R(3, 3) = 6. This means: if we want a complete graph that for any 2-coloring always has either [1] a clique of size 3 in the first color, or [2] a clique of size 3 in the second color, then we must have at least 6 vertices.
​
We know that R(4, 4) = 18, so here is a counterexample showing that R(4, 4) cannot be 17.
◼
Define a function that draws the 2-colored complete graph of 17 vertices whenever there is no clique of at least 4 vertices in either color, and also draws the colored components individually
◼
Construct a set of all edges on the complete graph of size 17 that are distance 1, 2, 4, or 8 from each other
◼
Test the counterexample
For comparison, here are some examples of 2-colored complete graphs of 18 vertices, all of which will have a clique of size 4 in at least one color.
◼
Define a function that draws the 2-colored complete graph of 18 vertices and highlight cliques of size 4 in either color with thick edges
◼
Define a filter that takes an edge set and drops each edge with probability 1/2
◼
Apply the function to one filtered edge set and magnify the picture by a factor of 3
◼
Apply the function to thirty filtered edge subsets
R(5, 5) is still unknown, although we currently know it is at least 43. Here is an example of a random 2-coloring on a complete graph of size 42 with the cliques of size 5 highlighted.
◼
Define a function that draws the 2-colored complete graph of 42 vertices and highlight cliques of size 5 in either color with thick edges
◼
Apply the function to one filtered edge set and magnify the picture by a factor of 3

Non-Diagonal Ramsey Numbers

We can generalize this to the non-diagonal case where the two parameters are different, meaning we require the cliques to be different sizes for each color. We know that R(3, 4) = 9, so here is a counterexample showing that R(3, 4) cannot be 8.
◼
Define a function that draws the 2-colored complete graph of 8 vertices whenever there is no clique of 3 vertices in one color and no clique of 4 vertices in the other, and also draws the colored components individually
◼
Construct a set of all edges on the complete graph of size 8 that are distance 1 or 4 from each other, removing duplicate edges
◼
Remove duplicate edges
◼
Test the counterexample
For comparison, here are some examples of 2-colored complete graphs of 9 vertices, all of which will have a clique of size 3 in red or a clique of size 4 in blue.
◼
Define a function that draws the 2-colored complete graph of 18 vertices and highlight red cliques of size 3 and blue cliques of size 4 with thick edges
◼
Apply the function to 30 filtered edges
Further Explorations
Generalized and Hypergraph Ramsey Numbers
Schur Numbers
Distributed Computing in Case of Alien Invasion
Authorship information
Dennis Hou
6/21/2017
smilax@gmail.com