You are using a browser not supported by the Wolfram Cloud
Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.
I understand and wish to continue anyway »
WOLFRAM NOTEBOOK
Gossip Algorithms over different network topologies
Gossip Algorithms over different network topologies
A brief description of three different gossip algorithms, Probabilistic Broadcast, Probabilistic Edge, Fixed Fanout, with detailed example on how do they work over different network topologies, Erdős–Rényi, Random Geometric Graph, scale free.
Random Graph
Random Graph
Gossip algorithms are a system of machine-to-machine communication whose goal is to minimize the channel usage and maximise the coverage of the network. Network can be seen as graph of nodes, nodes represent computers and edges represent connections.
◼
Example of a random graph:
In[1]:=
randomGraph=RandomGraph[{8,20}]
Out[1]=
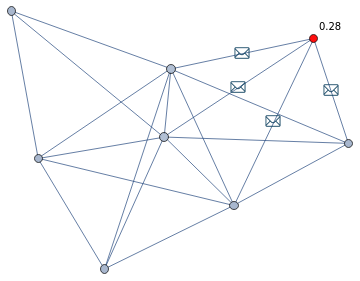
A pure mechanism of broadcast send the message to all the other node connected with the source, this method leads to a complete coverage of the message in the graph but on the other hand cause the saturation of the channel.
◼
In red the source of the message, mails on involved edges
In[2]:=
SetPropertySetProperty{randomGraph,EdgeList[randomGraph,1_]},EdgeLabels
,1,VertexStyleRed
Out[2]=
Symbols and Functions
Symbols and Functions
There are three famous gossip algorithm, their difference is mostly related on how do they choose the node to whom forward the messages. They are named in literature: Probabilistic Broadcast (PB), Probabilistic Edge (PE) e Fixed Fanout (FF).
In order to better understand the algorithms it’s important to introduce some notation
In order to better understand the algorithms it’s important to introduce some notation
◼
Λ
In[3]:=
Λ[graph_,i_]:=Map[Last,EdgeList[graph,i_]]1Λ[randomGraph,1]SetProperty[{SetProperty[randomGraph,VertexLabels"Name"],Λ[randomGraph,1]},VertexStyleYellow]
Out[4]=
1{2,4,5,8}
Out[5]=
◼
V
Λ
i
In[6]:=
V[graph_,i_]:=Length[Λ[graph,i]]V[randomGraph,1]
Out[7]=
4
◼
msg
p
v
p
e
Probabilistic Broadcast
Probabilistic Broadcast
The first algorithm is Probabilistic Broadcast, the value is the threshold that decide if the message will be send in broadcast or dropped from the node i .
p
v
◼
example of Probabilistic Broadcast with = 0.3
p
v
In[8]:=
ProbabilisticBroadcast[graph_,i_,msg_,pv_]:=With[{r=RandomReal[]},If[r≤pv,SetProperty[{SetProperty[{SetProperty[{graph,EdgeList[graph,i_]},EdgeLabelsmsg],i},VertexStyleRed],i},VertexLabels{SetPrecision[r,2]}],SetProperty[{SetProperty[{graph,i},VertexStyleRed],i},VertexLabels{SetPrecision[r,2]}]]]TableProbabilisticBroadcastrandomGraph,1,
,.3,{x,1,10}
Out[9]=
,
,
,
,
,
,
,
,
,
Probabilistic Edge
Probabilistic Edge
The second algorithm is Probabilistic Edge, the value is the threshold that decide if the message will be send on a specific arc or not, from the node i.
p
e
◼
example of edge selection with Probabilistic Edge with = 0.3
p
e
In[10]:=
GetEdge[graph_,i_,pe_]:=Map[First,Select[Map[With[{r=RandomReal[]≤pe},{#,r}]&,Map[i#&,Λ[graph,1]]],Last[#]True&]]GetEdge[randomGraph,1,.3]
Out[11]=
{14,15}
◼
example Probabilistic Edge with = 0.4
p
e
In[12]:=
Clear[ProbabilisticEdge]ProbabilisticEdge[graph_,i_,msg_,pe_]:=SetProperty[{SetProperty[{SetProperty[{graph,GetEdge[graph,i,pe]},EdgeLabelsmsg],i},VertexStyleRed],i},VertexLabels{SetPrecision[pe,2]}]TableProbabilisticEdgerandomGraph,1,
,.4,{x,1,10}
Out[14]=
,
,
,
,
,
,
,
,
,
Fixed Fanout
Fixed Fanout
The last algorithm is Fixed Fanout the node choose a number of random node connected with him to whom send the message.
Erdős–Rényi or Bernulli graph
Erdős–Rényi or Bernulli graph
The variance of vertex degree represent the variance of number of edge that each node are linked with.
It’s an important parameter that can impact in the spreading of the message a low variance in vertex degree can cause the dropping of a message before the coverage is complete.
It’s an important parameter that can impact in the spreading of the message a low variance in vertex degree can cause the dropping of a message before the coverage is complete.
The edge connectivity represent the minimum number of edge that should be deleted from a graph to make it disconnected.
Random Geometric Graph
Random Geometric Graph
◼
Variance of the vertex degree of a Random Geometric graph
◼
Edge connectivity of a Random Geometric graph
Example of Random Geometric graph
Example of Random Geometric graph
A typical example of Random Geometric graph are rails or highways, they share the same structure due two the fact that nears cities are commonly connected with a path.
◼
An example of highways graph of Italy city:
◼
The vertex degree is strictly related with political or economical influence and also with centrality in the map:
◼
An example of map of Italy highways with names of most connected city:
Scale Free graph
Scale Free graph
◼
Variance of the vertex degree of a Scale Free graph:
◼
Edge connectivity of a Scale Free graph:
Example of Scale Free graph
Example of Scale Free graph
◼
Internet is an example of Scale Free graph, here the info.cern.ch hyperlinks network:
Comparison between the graph topology
Comparison between the graph topology
It’s important to check the comparison between different aspect of each graph.
◼
Comparison of variance of the vertex degree between Erdős–Rényi, Random Geometric, and Scale Free graph:
◼
Comparison of edge connectivity between Erdős–Rényi, Random Geometric, and Scale Free graph
It can be seen in the previous graphs that each network has different behaviour over those important aspects.
Studying the mean of variation of vertex degree it can be understand better which graph has a more peculiar topology with high isolated nodes and cluster.
Studying the mean of variation of vertex degree it can be understand better which graph has a more peculiar topology with high isolated nodes and cluster.
◼
Random Geometric graph due to its unique topology shuld have the higher Variation of Vertex Degree, followed by Scale Free due to the presence of hub’s nodes, Erdős–Rényi on the other hand has a very low Vertex Degree variation.
It can also be compared the edge connectivity in order to properly understand the fault tolerance of those network and the reliability of the infrastructure.
◼
Scale Free graph do the presence of macro hub and clique has the higher edge connectivity, followed by Erdős–Rényi , and Random Geometric due to the isolated nodes.
Conclusion
Conclusion
Gossip Algorithms could be really useful in situation of network instability where the network topology change really fast, they can also be used to simulate human spreading of information and virus diffusion over population.
Further Explorations
Social Network
Torrent and Peer To Peer
Routing
Authorship information
Daniele Baschieri
20/06/2017
daniele.baschieri@gmail.com