The nine-point circle
The nine-point circle
Laney Moy
For any triangle, there exist nine significant concyclic points that lie upon what is known as the nine-point circle. The nine-point-circle has a host of interesting properties and relationships with other geometric aspects of a triangle. In this essay, we will explore the nine-point circle and its geometric properties.
What is the nine-point circle?
What is the nine-point circle?
The nine-point circle, also known as Euler’s circle or the Feuerbach circle, is defined by nine significant points of a triangle. Three of these points are the bases, or feet, of the altitudes dropped from each vertex of a triangle. The three altitudes intersect at the orthocenter. The midpoints of each side of the triangle also lie on the nine-point circle. The final three points along the nine-point circle are located halfway between each vertex and the orthocenter. These points are called the Euler points. Let’s take a look!
Construct a list of vertices for some triangle:
In[]:=
vertices={{0,0},{1,0},{0.7,0.6}};
Create a Manipulate to display different features of the triangle:
In[]:=
ManipulateGraphics,Style[Triangle[vertices],EdgeForm[Thickness[0.003`]],Transparent],If[all||n,Style[TriangleConstruct[vertices,"NinePointCircle"],Thick,Blue],Nothing],If[all||a,Style[TriangleConstruct[vertices,{"Altitude",#}]&/@vertices,Red],Nothing],If[all||o,Style[TriangleConstruct[vertices,"Orthocenter"],Darker@Red]],If[all||f,Style[TriangleConstruct[vertices,{"Foot",#}]&/@vertices,Red],Nothing],If[all||m,Style[TriangleConstruct[vertices,{"Midpoint",#}]&/@vertices,Darker@Green],Nothing],If[all||e,Style[Midpoint[{Point[#],Point@TriangleCenter[vertices,"Orthocenter"]}]&/@vertices,Purple],Nothing],Multicolumn,SaveDefinitionsTrue
Out[]=
The nine-point center and the Euler line
The nine-point center and the Euler line
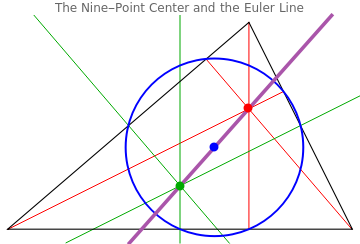
In a triangle, the circumcenter occurs at the intersection of the perpendicular bisectors. The Euler line is defined by the orthocenter and the circumcenter, through which it passes. The center of the nine-point circle, known as the nine-point center, also lies on the Euler line, halfway between the orthocenter and the circumcenter.
Calculate the nine-point center, orthocenter, and circumcenter:
In[]:=
npctr=Point@TriangleCenter[vertices,"NinePointCenter"];orthoctr=Point@TriangleCenter[vertices,"Orthocenter"];circumctr=Point@TriangleCenter[vertices,"Circumcenter"];
Display the nine-point circle and nine-point center (blue), altitudes and orthocenter (red), perpendicular bisectors and circumcenter (green), and Euler line (purple):
In[]:=
eulerLineGraphics=Graphics[{PointSize[0.025],Style[Triangle[vertices],EdgeForm[Thickness[0.003]],Transparent],Style[TriangleConstruct[vertices,"NinePointCircle"],Thick,Blue],Style[TriangleConstruct[vertices,"EulerLine"],Thickness[.01],Lighter@Purple],Style[npctr,Blue],Style[orthoctr,Red],Style[circumctr,Darker@Green]}];LegendedShow[Graphics[{Style[TriangleConstruct[vertices,{"Altitude",#}]&/@vertices,Red],Style[TriangleConstruct[vertices,{"PerpendicularBisector",#}]&/@vertices,Darker@Green]},PlotLabel"The Nine-Point Center and the Euler Line"],eulerLineGraphics],
Out[]=
A number of other notable triangle centers also lie on the Euler line, including the centroid of a triangle. The centroid is the center of mass of a region, assuming uniform density, and exists at the intersection of the medians of a triangle.
Display the nine-point circle and nine-point center (blue), medians and centroid (magenta), orthocenter (red), circumcenter (green), and Euler line (purple):
In[]:=
LegendedShow[Graphics[{PointSize[0.025],Style[{Point@TriangleCenter[vertices,"Centroid"],TriangleConstruct[vertices,{"Median",#}]&/@vertices},Magenta]},PlotLabel"The Nine-Point Center and the Euler Line"],eulerLineGraphics],
Out[]=
Relationship to the circumcircle
Relationship to the circumcircle
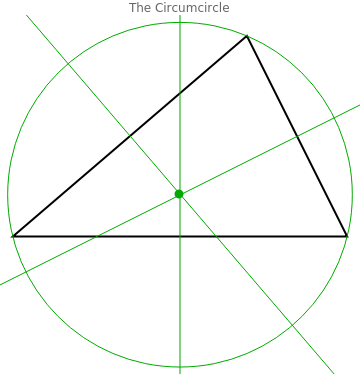
The circumcenter, which we recently observed, is so named because it is the center of the circumcircle containing the triangle.
Display the perpendicular bisectors, circumcenter, and circumcircle:
In[]:=
LegendedGraphics[{Style[Triangle[vertices],EdgeForm[Thick],Transparent],PointSize[0.025],Style[{TriangleConstruct[vertices,"Circumcircle"],TriangleConstruct[vertices,{"PerpendicularBisector",#}]&/@vertices,circumctr},Darker[Green]]},PlotLabel"The Circumcircle"],
Out[]=
The radius of the nine-point circle is exactly half the radius of the circumcircle.
Display the nine-point center and nine-point circle (blue), as well as the circumcenter and circumcircle (green), and print the radii of the two circles:
In[]:=
LegendedGraphics[{Style[Triangle[vertices],EdgeForm[Thick],Transparent],PointSize[0.025],Style[{TriangleConstruct[vertices,"NinePointCircle"],npctr},Blue],Style[{TriangleConstruct[vertices,"Circumcircle"],circumctr},Darker[Green]]},PlotLabel"The Nine-Point Circle and the Circumcircle"],Print["Circumradius: ",TriangleMeasurement[vertices,"Circumradius"]]Print["Nine-point radius: ",TriangleMeasurement[vertices,"NinePointRadius"]]
Out[]=
The nine-point circle as a circumcircle
The nine-point circle as a circumcircle
Because the nine-point circle contains the medians of each side of the reference triangle and the feet of the altitudes, the nine-point circle serves as a circumcircle for the medial and orthic triangles.
Display the medial triangle (green), orthic triangle (red), and nine-point circle (blue):
Feuerbach’s Theorem
Feuerbach’s Theorem
The incircle of a triangle is internally tangent to all three sides of the triangle.
Display the incircle:
The three excircles of a triangle are externally tangent to each side of the reference triangle and to the infinite lines extending from the other two sides.
Display the three excircles:
According to Feuerbach's Theorem, the nine-point circle is internally tangent to the incircle and externally tangent to all three excircles of the reference triangle.
Display the nine-point circle (blue), incircle (brown), and excircles (pink):
The nine-point circle in an orthocentric system
The nine-point circle in an orthocentric system
An orthocentric system is a set of four points in which each point serves as the orthocenter for the triangle formed by the other three. In an orthocentric system, the all four possible triangles formed by three of the points share a nine-point circle.
To create an orthocentric system, we can take an arbitrary triangle and find the orthocenter, which will be the fourth point.
Create and display an arbitrary orthocentric system:
Each of these triangles has the same nine-point circle.
Calculate and display the nine-point circle for each triangle in the orthocentric system:
Recall that the radius of the nine-point circle is exactly half of the radius of the circumcircle. Because each of the four triangles in an orthocentric system has the same nine-point circle, the circumcircles of each must have equal radii.
For each triangle in the orthocentric system, show the circumcircle and label with its radius:
Display all four circumcircles (orange) along with the nine-point circle (blue) and the radii of each:
Given any triangle, the centers of the excircles and incircles form an orthocentric system.
Generate an arbitrary triangle and calculate the incenter and excenters:
Display the orthocentric system formed by the incenter and excenters:
Recall that the nine-point circle of a triangle is also the circumcircle of its orthic triangle. The nine-point circle of this orthocentric system is the circumcircle of the original triangle.
Display the nine-point circle of the orthocentric system, which is also the circumcircle of the original triangle:
Conclusion
Conclusion
The nine-point circle of a triangle has a number of properties from its use as a circumcircle to its relations to an orthocentric system. Examining the nine-point circle leads to a variety of interesting visualizations and relationships to other triangles and circles.