Wolfram Summer School 2018: Resolution Based Automated Theorem Prover for First Order Logic
Author
Jan Stańczuk
Title
Wolfram Summer School 2018: Resolution Based Automated Theorem Prover for First Order Logic
Description
Wolfram Summer School 2018: Resolution Based Automated Theorem Prover for First Order Logic
Category
Essays, Posts & Presentations
Keywords
Wolfram Summer School 2018
URL
http://www.notebookarchive.org/2018-12-53xj96l/
DOI
https://notebookarchive.org/2018-12-53xj96l
Date Added
2018-12-11
Date Last Modified
2018-12-11
File Size
1.61 megabytes
Supplements
Rights
Redistribution rights reserved

WOLFRAM SUMMER SCHOOL 2018
Last modified on: Wednesday, July 11, 2018 at 3:13
Author Info
Name:
Jan Stańczuk
Mentor:
Christopher Wolfram
Affiliation:
King’s College London
Poster Session Content
Title of project:
Resolution Based Automated Theorem Prover for First Order Logic
Goal of the project:
The goal of the project was to implement a simple resolution based theorem prover for first order logic in the Wolfram Language, including Skolemization and Most General Unification.
Add the most representative image of your project here. (We recommend just 1 image, if you add more, we will make a collage of the images.)
Image:
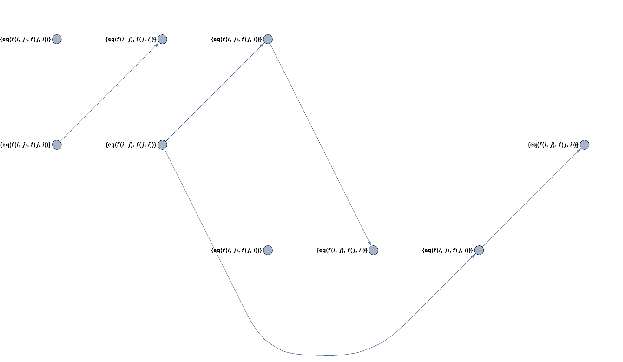
Summary of Results:
In order to be able to apply the resolution method to an arbitrary sentence in first order logic, one must first convert it to conjunctive normal form (CNF). I began my project by implementing the necessary components of the conversion including conversion to prenex normal form and elimination of existential quantifiers using Skolemization. Afterwards, I implemented the most general unification algorithm, which is a central part of a resolution based theorem prover. Having all the components in place I implemented the resolution algorithms using two resolution strategies, Set of Support and Linear Resolution, thereby completing the implementation of the theorem prover.
The resulting implementation provides a complete semi-decision procedure for first order logic.
In principle given infinite time and memory the theorem prover could find a proof of any theorem entailed by the given set of axioms.
The resulting implementation provides a complete semi-decision procedure for first order logic.
In principle given infinite time and memory the theorem prover could find a proof of any theorem entailed by the given set of axioms.
Future work:
Although resolution provides a refutation-complete method for theorem proving, the time required to prove complicated theorems would be extremely high due to a combinatorial explosion of the search space. In order to be able to prove such results one must restrict the search space and remove redundancies by applying optimizations and heuristics on top of the pure resolution method. Some of the logical improvements would include implementation of subsumption, tautology deletion, Knuth-Bendix ordering, paramodulation and unit preference. These could drastically improve the performance of the theorem prover.
Lastly it would be an intriguing idea to combine the resolution theorem prover with Mathematica FindEquationalProof function.
Lastly it would be an intriguing idea to combine the resolution theorem prover with Mathematica FindEquationalProof function.
Note
: Everything above this bar is your poster.Make sure it fits on a single page. Preview Poster
End of School Presentation Content
In addition to the poster content, include other content to present at the 2 minute presentation for end of school. Use the buttons below to add more sections.
Add Header
Add Text
Add Code or Image
Example Proof
Given: f(x,y) = f(y,x) and axioms of equality
Prove: f(f(a,b),f(c,d)) = f(f(d,c), f(b,a))
Prove: f(f(a,b),f(c,d)) = f(f(d,c), f(b,a))
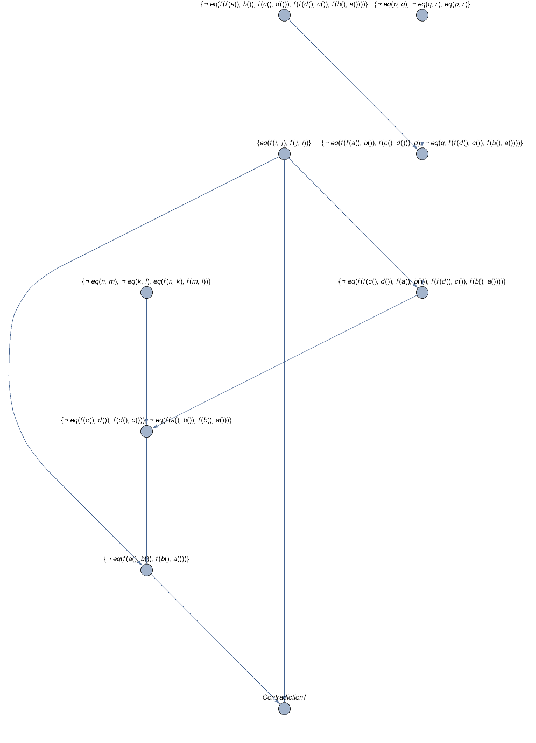
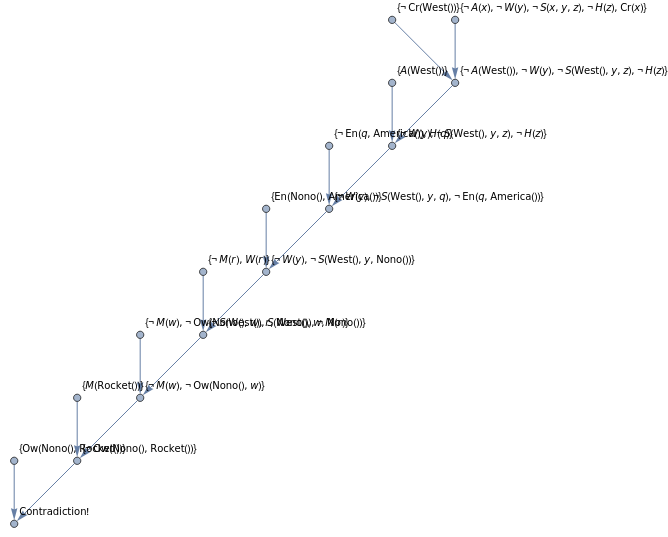
Example Proof 2
The law says that it is a crime for an American to sell weapons to hostile nations.The
country Nono, an enemy of America, has some missiles, and all of its missiles were sold
to it by Colonel West, who is American.
country Nono, an enemy of America, has some missiles, and all of its missiles were sold
to it by Colonel West, who is American.
Note
: Everything above this bar is in your 2 minute presentation. Make sure it fits on 2 slides. Preview Presentation
Detailed Project Notes
Main Results in Detail
Main Results in Detail
The resulting implementation of a theorem prover provides a complete semi - decision procedure for first order logic. In principle given infinite time and memory the theorem prover could find a proof of any theorem entailed by the given set of axioms.
Code
Code
All Visualizations
All Visualizations
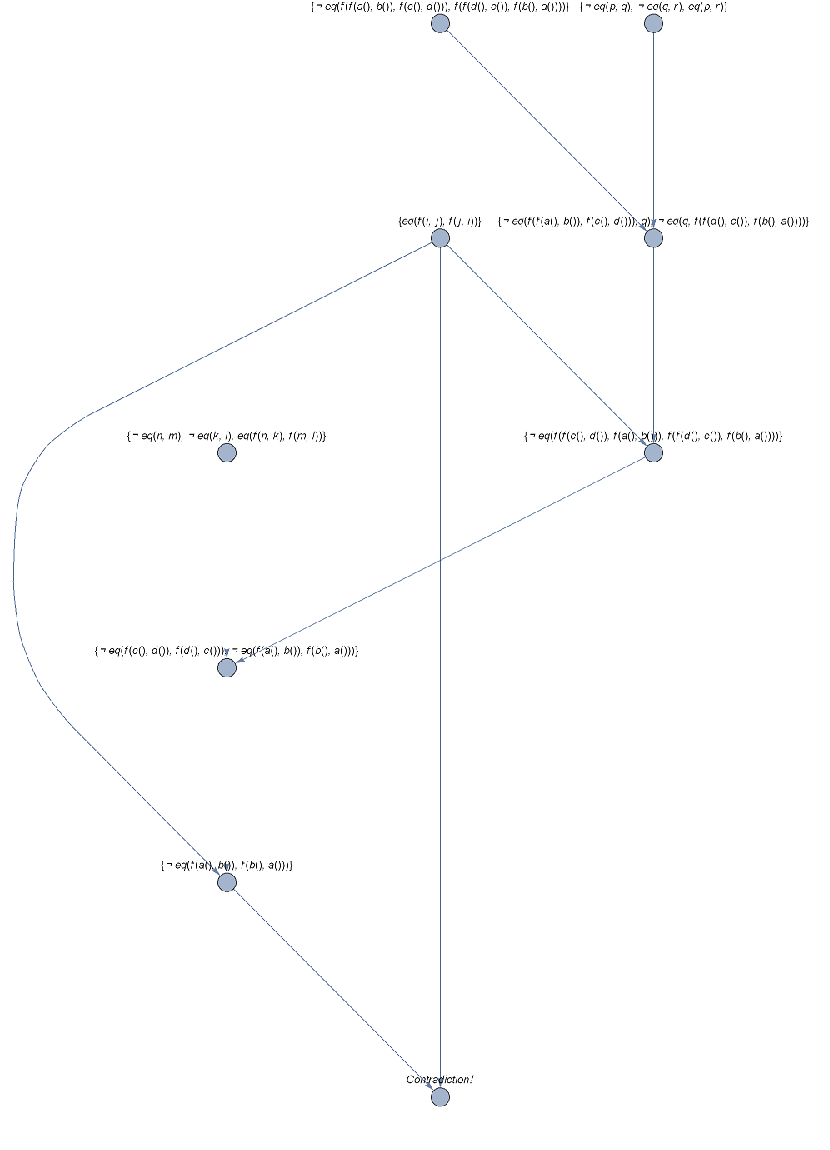
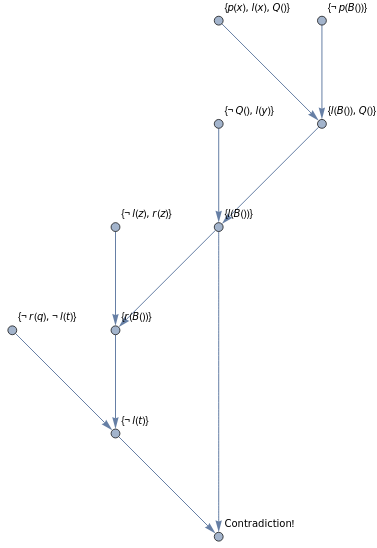

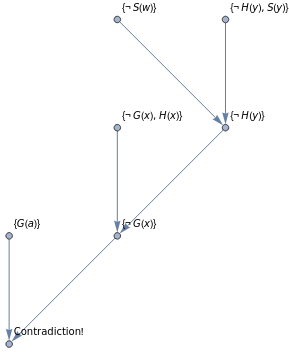
Data Sources Links/References
Data Sources Links/References
◼
J. Alan Robinson, Andrei Voronkov, Handbook of Automated Reasoning
◼
Peter Norvig, Stuart J. Russell, Artificial Intelligence: A Modern Approach
◼
Chang, Lee, Symbolic Logic and Mechanical Theorem Proving
Future Directions
Future Directions
Although resolution provides a refutation - complete method for theorem proving, the time required to prove complicated theorems would be extremely high due to a combinatorial explosion of the search space. In order to be able to prove such results one must restrict the search space and remove redundancies by applying optimizations and heuristics on top of the pure resolution method. Some of the logical improvements would include implementation of subsumption, tautology deletion, Knuth - Bendix ordering, paramodulation and unit preference. These could drastically improve the performance of the theorem prover.
Lastly it would be an intriguing idea to combine the resolution theorem prover with FindEquationalProof
Lastly it would be an intriguing idea to combine the resolution theorem prover with FindEquationalProof
Other information
Other information
Cite this as: Jan Stańczuk, "Wolfram Summer School 2018: Resolution Based Automated Theorem Prover for First Order Logic" from the Notebook Archive (2018), https://notebookarchive.org/2018-12-53xj96l
Download
