Triangular and pyramidal numbers
Triangular and pyramidal numbers
Bill Gosper
f(n)=”The triangular numbers”=1+2+ . . .+n.Using 9 for n,
Graphics[{PointSize[Large],Point[Permutations[Range@9,{2}]]}]
I.e.,the unequal pairs of numbers up to 9 plots as a 9×9 square minus
its length 9 diagonal. But this is just two copies of 1+ . . .+8. So
its length 9 diagonal. But this is just two copies of 1+ . . .+8. So
2f(n-1)-n;
2
n
Solving for f(n)
RSolve[%,f[n],n]//Factor
f[n]n(1+n)
1
2
This is essentially how the Gauß, the youngster, startled his grammar school teacher.
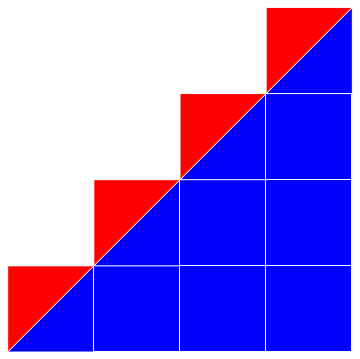
In highschool, my friend Reed Carson and I got this a different way—by adding up the areas of n+1 triangles:
In highschool, my friend Reed Carson and I got this a different way—by adding up the areas of n+1 triangles:
Table[{x,y},{x,4},{y,x}]
{{{1,1}},{{2,1},{2,2}},{{3,1},{3,2},{3,3}},{{4,1},{4,2},{4,3},{4,4}}}
Graphics[{EdgeForm[White],Blue,%/.{x_Integer,y_}->Rectangle[{x,y}]}]/.{L___,Rectangle[{x_Integer,y_}]}{L,Triangle[{{x,y},{x+1,y},{x+1,y+1}}],Red,Triangle[{{x,y},{x,y+1},{x+1,y+1}}]}
Now for 3D. Using as coordinates the integers 1, 2, ..., n taken three at a time,
Graphics3D[Sphere[Permutations[Range@9,{3}],1/2]]
The unequal triads of numbers up to 9 plots as a 9×9×9 cube minus
those diagonals which have two or three coordinates the same:
those diagonals which have two or three coordinates the same:
Graphics3D[Sphere[Select[Tuples[Range@9,3],Not[UnsameQ@@#]&],1/2]]
This is six triangulars of size 8 (= n-1) plus the central column of 9 (=n).
The former is six pyramids of size 7 (= n-2). Together they make a cube of size n=9.
So the equation for the pyramidal numbers solves as
The former is six pyramids of size 7 (= n-2). Together they make a cube of size n=9.
So the equation for the pyramidal numbers solves as
RSolve[6f[n-2]+6n(n-1)/2+nn^3,f[n],n]//Factor
f[n]n(1+n)(2+n)
1
6
Instead of 1 + 3 + 6 + . . . + n, summing 1² + 2² + . . . + n² gives the “square pyramidal numbers”,
Table[Sphere[{x,y,z},1/2],{z,7},{y,z},{x,z}]//Graphics3D
each of which is the sum of two consecutive ordinary pyramidal numbers:
%/.Sphere[{x_,y_,z_},1/2]Sphere[{x,y,z},1/4]/;x<y
So the sum of the first n squares, 1² + 2² + . . . + n², is
(You can also see that each square (each layer) is the sum of two consecutive triangular numbers.)
But, as before, my friend Reed and I got this geometrically, as the the sum of a big pyramid plus two triangular arrays of half-cubes, plus n “notched” cubes (shown transparent) running up the long diagonal, each notch being a little pyramid of volume ⅓:
But, as before, my friend Reed and I got this geometrically, as the the sum of a big pyramid plus two triangular arrays of half-cubes, plus n “notched” cubes (shown transparent) running up the long diagonal, each notch being a little pyramid of volume ⅓:
For 5 = n, the volume of this is big pyramid + n notched cubes + two triangles of half-cubes , or
(For this problem, we don’t need to know that the volume of a pyramid is always ⅓ the volume of its circumscribing prism, because a cube can always dissect into three copies of the (square based) pyramid we’re discussing.)
--Bill