Zeros of a Polynomial or Rational Function and Its Derivative
Zeros of a Polynomial or Rational Function and Its Derivative
This Demonstration shows the connection between the real zeros of a function and those of its derivative . It is also shown that for rational functions, the asymptotes of the function match those of the derivative.
f(x)
f'(x)
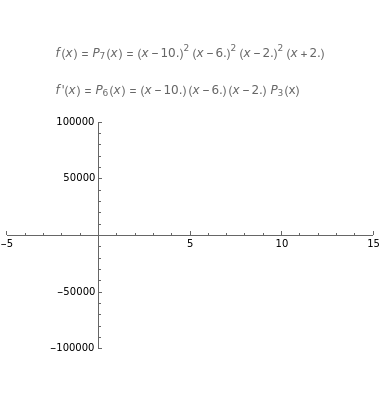
When is a polynomial, a zero of of multiplicity is a zero of with multiplicity .
f(x)
f(x)
m>1
f'(x)
m-1
If
f(x)=(x)=⋯
P
n
k
0
(x-)
x
0
k
1
(x-)
x
1
k
s
(x-)
x
s
where =n and the are distinct, then is the number of distinct zeros, and
s
∑
i=0
k
i
x
i
s
f'(x)=(x)=-1-1⋯-1(x)
P
n-1
k
0
(x-)
x
0
k
1
(x-)
x
1
k
m
(x-)
x
m
P
s-1
where (x) introduces additional zeros.
P
s-1
s-1
In the case of a rational function, the rule becomes:
f(x)=(x)=⋯
P
n
Q
m(x)
k
0
(x-)
x
0
k
1
(x-)
x
1
k
s
⋯(x-)
x
s
v
0
(x-)
z
0
v
1
(x-)
z
1
v
p
(x-)
z
p
where =n, =m, the are distinct, the are distinct, and
s
∑
i=0
k
i
p
∑
j=0
v
j
x
i
z
j
f'(x)=(x)(x)=-1-1⋯-1-1-1⋯-1(x)⋯
P
m+n-1
Q
2m
k
0
(x-)
x
0
k
1
(x-)
x
1
k
s
(x-)
x
s
v
0
(x-)
z
0
v
1
(x-)
z
1
v
p
(x-)
z
p
P
s+p-1
2
v
0
(x-)
z
0
2
v
1
(x-)
z
1
2
v
p
(x-)
z
p
where is the number of distinct zeros of the numerator and is the number of distinct zeros of the denominator.
s
p
When the rule becomes:
n=m
f(x)=(x)=⋯
P
m
Q
m(x)
k
0
(x-)
x
0
k
1
(x-)
x
1
k
s
⋯(x-)
x
s
v
0
(x-)
z
0
v
1
(x-)
z
1
v
p
(x-)
z
p
where
s
∑
i=0
k
i
p
∑
j=0
v
j
f'(x)=(x)(x)=-1-1⋯-1-1-1-1(x)⋯
P
2m-1
Q
2m
k
0
(x-)
x
0
k
1
(x-)
x
1
k
s
(x-)
x
s
v
0
(x-)
z
0
v
1
(x-)
z
1
v
p
⋯(x-)
z
p
P
s+p-2
2v0
(x-)
z
0
2v1
(x-)
z
1
2vp
(x-)
z
p
where is the number of distinct zeros of the numerator and is the number of distinct zeros of the denominator.
s
p
That is to say, the derivative will have one fewer zero and the asymptotes will remain.
The zeros of the are highlighted with , while the zeros of the are highlighted with ; in the case of a rational function, the vertical asymptotes are marked by .
f(x)
●
f'(x)
x
----
The top popup menu selects between the polynomial or rational function. In the case of a polynomial function, the controls let you vary the constant terms , , and , as well as the degree of each binomial factor. In the case of a rational function, the controls let you vary the constant terms and , as well as the degree of each binomial in the numerator, and the constant terms and , as well as the degree of each binomial in the denominator. There are sliders to let you vary the scale of the graph. The bottom part includes checkboxes to highlight specific parts of the Demonstration.
x
0
x
1
x
2
x
4
x
0
x
1
z
0
z
1