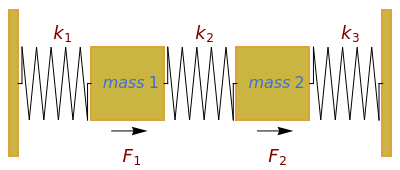WOLFRAM NOTEBOOK

WOLFRAM|DEMONSTRATIONS PROJECT

Two Masses with Forcing Functions Oscillating between Three Springs

​
initial displacements
x
1
0
x
2
0
forcing frequencies
ω
1
Pi
ω
2
Pi
release system
This Demonstration treats a system consisting of three springs connecting two masses between two walls with forcing functions on the masses, given by
F
1
=5cos(
ω
1
t)
and
F
2
=5cos(
ω
2
t)
. The solution plots are shown and dynamically updated to reflect changes to the initial displacements and the forcing frequencies. The short-term behavior can be affected by the changes in initial displacement, but the long-term behavior is dominated by the forcing functions. The two equations being solved are:
2
d
x
1
(t)
d
2
t
=
1
m
1
(
k
1
+
k
2
)
x
1
(t)-
k
2
m
1
x
2
(t)=5cos(
ω
1
t)
,
2
d
x
1
(t)
d
2
t
=
1
m
2
(
k
2
+
k
3
)
x
2
(t)-
k
2
m
2
x
1
(t)=5cos(
ω
2
t)
.
Wolfram Cloud

You are using a browser not supported by the Wolfram Cloud

Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.


I understand and wish to continue anyway »

You are using a browser not supported by the Wolfram Cloud. Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.