Trisecting an Angle Using a Lemniscate

fix angle α to trisect

translate to touch

labels when tangent

show angle to trisect

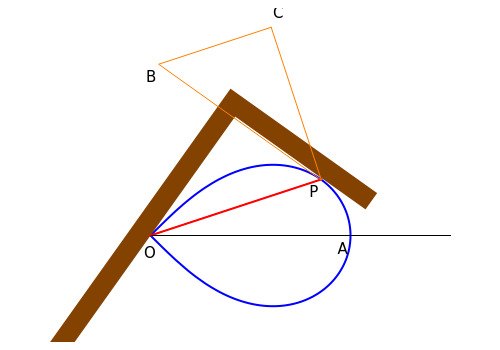
The angle to trisect, say

, is between the longer leg of the carpenter's square (the brown "L" shape) and the polar axis

. Translate the carpenter's square so that it touches the curve at the point

. The angle

AOP

between the radius vector

and the polar axis

is one-third of the given angle

For any curve in polar coordinates, the tangent of the angle

between the tangent and radial line (the angle between vectors

and

) at the point

(r,θ)

tan(β)=r/r'

. The lemniscate has the polar equation

r=

cos(2θ)

, and the derivative with respect to

r'=

-sin(2θ)



cos(2θ)

, so

r/r'=

cos(2θ

-sin(2θ)



cos(2θ)

=-cot(2θ)

. So

tan(β)=-cot(2θ)=-tan(π/2-2θ)=tan(2θ-π/2)

. Since

is obtuse,

β=2θ+π/2

∠OPB=π-β=π/2-2θ

, and the angle

BPC

between the tangent

and the normal

to the radius vector

2θ

. But this angle

BPC

is equal to the angle between the larger leg of the carpenter's square and the radius vector

, because these angles have orthogonal legs. So

α-θ=2θ

α=3θ