Time-Dependent Superposition of Particle-in-a-Box Eigenstates

expansion coefficients

c

1

0.8

c

2

0.

c

3

0.

c

4

0.

c

5

0.

c

6

0.

time

0.

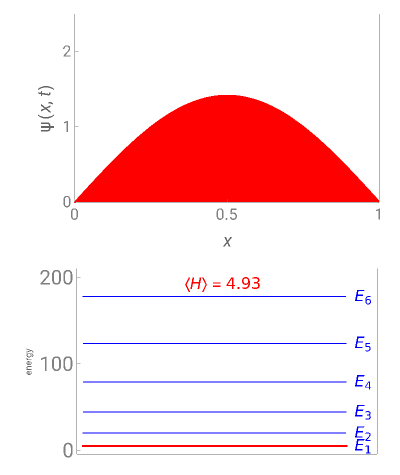
This Demonstration looks at a time-dependent superposition of quantum particle-in-a-box eigenstates,

ψ(x,t)=

6

∑

n=1

c

n

-

E

n

t/ℏ

e

ϕ

n

(x)

, where the eigenstates and eigenenergies are given by

ϕ

n

(x)=

2

L

sin

nπx

L

and

E

n

=

2

n

2

π

2

ℏ

2m

2

L

, respectively. The Hamiltonian for this system is



H

=

2



p

2m

, and its expectation value gives the energy





H

=

ψ(x,t)



H

ψ(x,t)

〈ψ(x,t)ψ(x,t)〉

. The upper panel shows the complex wavefunction

ψ(x,t)

, where the shape is its modulus and the coloring is according to its argument (the range

0

to

2π

corresponds to colors from red to magenta). The lower panel shows the eigenenergies in blue and the energy of the superposition state in red.