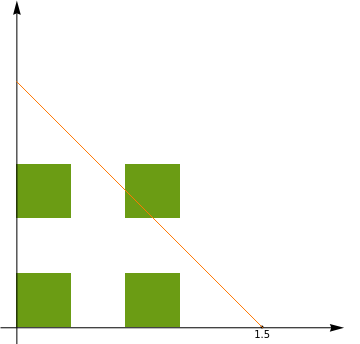The Sum of Two Cantor Sets

a

1.5

Cantor level

1

The Cantor set

C

is constructed iteratively. Starting with the closed unit interval

[0,1]

, the open middle third

1

3

,

2

3

is taken out, leaving the two closed intervals

0,

1

3



and



2

3

,1

. Then the middle thirds of those two intervals are taken out, leaving four intervals of length

1

9

, and so on. The Cantor set is the limit (or intersection) of all such sets.

Even though the Cantor set has measure zero and is nowhere dense, the set of sums

x+y

where

x

and

y

are in

C

is the whole interval

[0,2]

, because the line

x+y=a

always intersects the set

C×C

.