The Quantum Harmonic Oscillator with Time-Dependent Boundary Condition in the Causal Interpretation

time steps

25

amplitude q

1

5

box length L

3

frequency ω

3

quantum number m

1

2

3

potential type

1

2

3

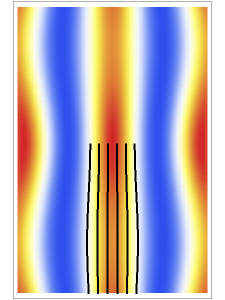
One of the challenging aspects of quantum mechanics is to derive the classical world from the quantum world. In this Demonstration, we discuss the dynamics of quantum particles bouncing between two oscillating infinitely high walls. The shape of the bottom of the well is described by a harmonic oscillator potential with a time-dependent frequency

2

Ω

. In the causal approach, the quantum potential governs the dynamics of the quantum particle; the link between classical Newtonian mechanics and the quantum world is the quantum potential. The total effective potential is the sum of the potential

V

and the quantum potential (

QP

), which leads to the time-dependent quantum force. In a single nonstationary state the quantum particles in the ensemble therefore behave classically in spite of having an associated wave function that satisfies the Schrödinger equation.

The graphics show the squared wavefunction and the trajectories in

x

-

t

space on the right, and on the left the position of the particles, the squared wavefunction (blue), the total effective potential (red), and the harmonic potential (cyan). The potentials are appropriately scaled to fit.