The Plemelj Triangle via the Fixed Point of a Transformation
The Plemelj Triangle via the Fixed Point of a Transformation
This problem was posed to Plemelj by his math teacher Borstner when Plemelj was about 16 years old. The problem asks for the construction of a triangle using ruler and compass given the length of the base , the length of the altitude from to , and , where and are the angles at and . In this Demonstration, and =1.
ABC
AB=c
h
c
C
AB
α-β
α
β
A
B
c=1
h
c
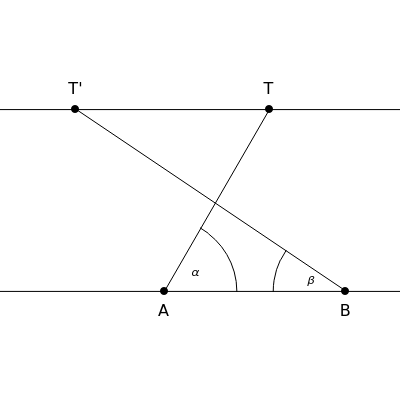
Draw two parallel lines separated by a distance =1. Mark off the line segment of length on the lower parallel line. The line drawn through with angle intersects the upper parallel line at , and the line through with angle intersects the upper parallel line at . What is the relationship between and ?
h
c
AB
c=1
A
α
T
B
β
T'
T
T'
Introduce a coordinate system with the origin at and the axis along so that . The line has the equation , and has the equation . Let and . Then, using the addition formula for the tangent gives the following formulas for the abscissas of and :
A
x
AB
B=(1,0)
AT
y=xtanα
BT
y=-(x-1)tanβ
a=tanα
d=tan(α-β)
T
T'
x=1/a
x'=((d+1)x+(d-1))/(dx-1)
or
x=
1
a
x'=
(d+1)x+(d-1)
dx-1
So the construction problem is to find the fixed point of the transformation to give . For this to happen, . If , this equation has the solution . In this Demonstration, we take the solution with the minus sign. Geometrically, the fixed point is determined by the values of and such that points and are coincident.
x=x'
d-(d+2)-(d-1)=0
2
x
d≠0
1/(2d)(d+2)±
5+4
2
d
α
β
B
B'
Since quadratic equations can be solved by construction with a straight edge and a compass, Plemelj's problem has a purely geometric solution.