WOLFRAM|DEMONSTRATIONS PROJECT

The Plemelj Construction of a Triangle: 2

c

h

C

δ = α-β

0.7

steps

1

2

3

4

verification

plot range

1

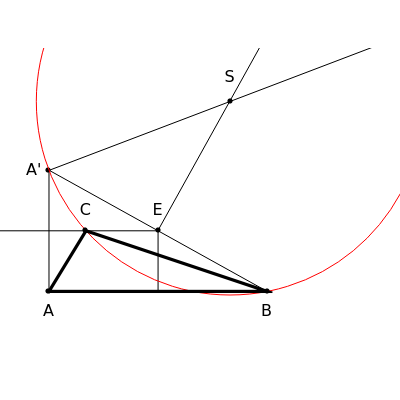
This Demonstration constructs a triangle

ABC

given the length

AB=c

of its base, the length

h

C

of the altitude from

C

to

AB

and the difference

α-β

between the angles at

A

and

B

.

Construction

Step 1: Draw a line segment

AB

of length

c

. Draw the line segment

AA'

of length

2

h

C

perpendicular to

AB

. Let

E

be the midpoint of

A'B

.

Step 2: Construct a circle

σ

such that the chord

A'B

subtends an angle

δ

from points on

σ

above the chord. Let

S

be the center of

σ

. The corresponding central angle

∠A'SB=2δ

.

Step 3: Let

C

be the intersection of

σ

and the line through

E

parallel to

AB

.

Step 4: The triangle

ABC

meets the stated conditions.

Verification

Let

D

be the midpoint of

AB

. By construction,

AA'=2

h

C

, so

DE=

h

C

.

By construction,

AB=c

, and the altitude from

C

to

AB

has length

h

C

.

It remains to prove

δ=α-β

.

Let the angle at

C

be

γ

. Consider these three angles around the point

C

:

∠ACA'

,

∠A'CB

and

∠ACB=γ

, which sum to

2π

. Since

CE

is parallel to

AB

and

E

is the midpoint of

A'B

,

CE

is the perpendicular bisector of

AA'

,

ACA'

is isosceles,

CE

bisects

∠ACA'

and alternate angles around

AC

imply

∠ACA'=2α

. Therefore

∠A'CB=2π-2α-γ

. Since

α+β+γ=π

,

∠A'CB=2π-2α-(π-α-β)=π+β-α

. (1)

On the other hand, the chord

A'B

subtends the angle

δ

from any point

F

on

σ

above

AB

:

∠A'BF=δ

. The quadrilateral

A'CBF

is cyclic, so its opposite angles are supplementary:

∠A'CB+∠A'BF=π

or

∠A'CB=π-δ

. (2)

From (1) and (2),

π+β-α=π-δ

, so

δ=α-β

.