The Natural Logarithm is the Limit of the Integrals of Powers
The Natural Logarithm is the Limit of the Integrals of Powers
Assume that and that .
a≠0
x>0
The integral of is +C, where is an arbitrary constant. The integral of = is , where again is an arbitrary constant and is the natural logarithm of , often written as .
a-1
x
a
x
a
C
-1
x
1
x
log(x)+C'
C'
log(x)
x
ln(x)
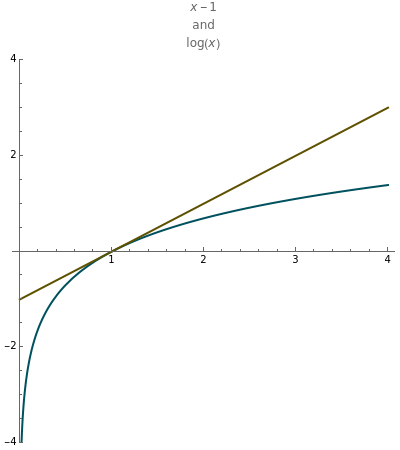
When is close to zero, and are close, so there must be some connection between their integrals!
a
a-1
x
-1
x
Choose and so that the two integrals are both zero at . The integrals are then - and . For close to zero these functions are very close; in symbols, -=log(x).
C=-
1
a
C'=0
x=1
a
x
a
1
a
log(x)
a
lim
a0
a
x
a
1
a
Using the difference quotient for the derivative of the base- exponential function with respect to (not ) and using instead of the more usual gives . This is more usually written with as the variable: =log(u), with the special case =.
x
f(b)=
b
x
b
x
a
h
f'(b)==-=-1=log(x)
lim
a0
f(b+a)-f(b)
a
lim
a0
b+a
x
b
x
a
b
x
lim
a0
a
x
a
b
x
x
d
dx
x
u
x
u
d
dx
x
e
x
e