The Kappa Curve as a Locus

θ

1

a

2

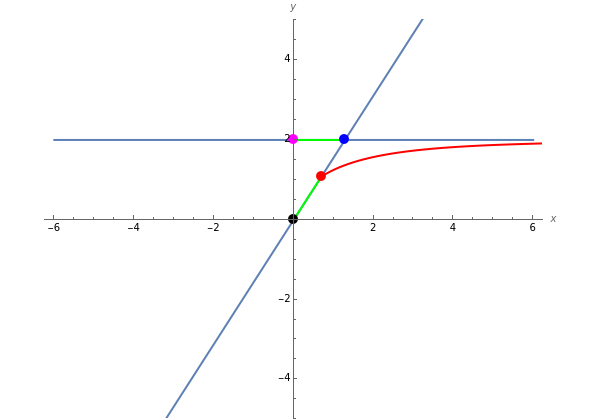
The kappa curve looks vaguely like a curly kappa,

ϰ

, and was studied by Newton, Bernoulli, and Gutschoven. Sometimes called Gutschoven's curve, its double cusp form can be represented as

2

y



2

x

+

2

y

=

2

a

2

x

.

Let

R

be the point

(0,a)

(magenta). Let

S

be the intersection point (blue) of the horizontal line

y=a

with a line

y=xtan(θ)

rotating about the origin

O

. The kappa curve is the locus of points

P

(red) on the rotating line such that distances

OP=RS

(green segments).