The Intersections of Extended Cevians with Three Circumcircles of Subtriangles

AP	≈	2.24	BP	≈	7.39	CP	≈	3.07
AX	≈	11.05	BY	≈	14.76	CZ	≈	10.35

AP

AX

+

BP

BY

+

CP

CZ

≈

1.00

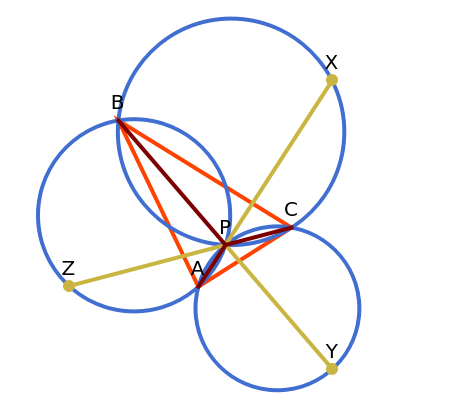
Let P be a point in the interior of the triangle ABC. Draw the three circumscribed circles for the triangles APB, APC, and BPC. Let X, Y, and Z be the intersections (other than P) of the extensions of AP, BP, and CP with the circles opposite A, B, and C. Then:

AP

AX

+

BP

BY

+

CP

CZ

=1

.