The Hydrogen Atom in Parabolic Coordinates
The Hydrogen Atom in Parabolic Coordinates
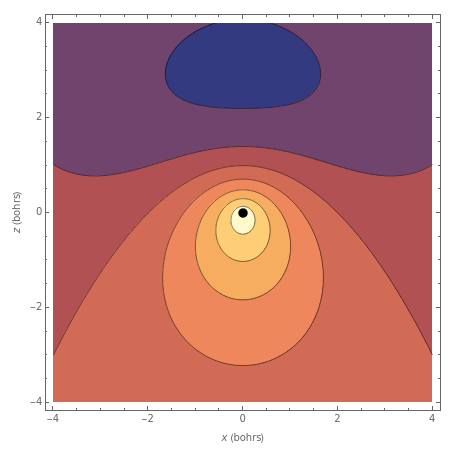
The Schrödinger equation for the hydrogen atom, (in atomic units ), can be separated and solved in parabolic coordinates as well as in the more conventional spherical polar coordinates . This is an indication of degeneracy in higher eigenstates and is connected to the existence of a "hidden symmetry", namely the Lie algebra associated with the Coulomb problem. Parabolic coordinates can be defined by , , with the same as in spherical coordinates. The wavefunction is separable in the form m(ξ,η,ϕ)=N(ξ)(η)with (ζ)=+,(ζ/n). Here is a Whittaker function and , equal to the principal quantum number. Contour plots for the real part of the wavefunctions in the -plane are shown, including the values and . The nucleus is represented as a black dot. The corresponding energy eigenvalues are given by =-, independent of other quantum numbers (in the field-free nonrelativistic case).
-ψ(r)-ψ(r)=Eψ(r)
1
2
2
∇
1
r
ℏ=m=e=1
(ξ,η,ϕ)
(r,θ,ϕ)
SO(4)
ξ=r(1+cosθ)=r+z
η=r(1-cosθ)=r-z
ϕ=arctan(y/x)
ψ
n
1
n
2
f
1
f
2
imϕ
e
f
1,2
-1/2
ζ
M
n
1,2
|m|+1
2
|m|
2
M
n=++|m|+1
n
1
n
2
x,z
ϕ=0
π
E
n
1
2
2
n
The hydrogen atom in a constant electric field ℰ along the direction is also separable in parabolic coordinates and can thus be used to treat the Stark effect. The functions (ξ) and (η) are more complicated but can be obtained by perturbation expansions. To first order, the Stark effect energies are given by ≈-+ℰn(-). One atomic unit of electric field ℰ is equivalent to V/m. The presence of an electric field is shown by a red arrow.
z
f
1
f
2
E
n
n
1
n
2
1
2
2
n
3
2
n
1
n
2
5.142×
11
10