WOLFRAM|DEMONSTRATIONS PROJECT

The Györgyi-Field Model for the Belousov-Zhabotinsky Reaction

​
k
f
0.00039
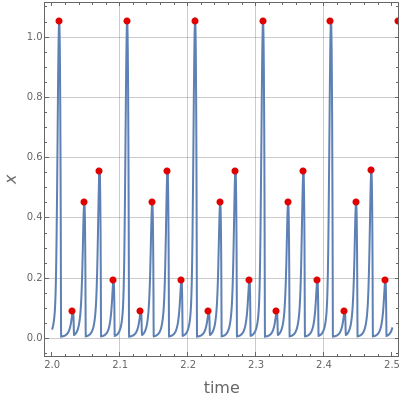
The Belousov–Zhabotinsky (BZ) reaction in a continuous-flow stirred-tank reactor (CSTR) can exhibit chaos, contrary to the Oregonator model, which has no chaotic solutions.
Deterministic chaos in the BZ reactor was studied in [1]. The scaled differential equations are:
dx
dτ
=
T
0
-
k
1
H
Y
0
x

y
+
k
2
A
2
H
Y
0

X
0

y
-2
k
3
X
0
2
x
+0.5
k
4
0.5
A
1.5
H
-0.5
X
0
(C-
Z
0
z)
0.5
x
-0.5
k
5
Z
0
xz-
k
f
x
,
dz
dτ
=
T
0

k
4
0.5
A
1.5
H
0.5
X
0
(C/
Z
0
-z)
0.5
x
-
k
5
X
0
xz-α
k
6
V
0
zv-β
k
7
Mz-
k
f
z
,
dv
dτ
=
T
0
2
k
1
H
X
0
Y
0

V
0
x

y
+
k
2
A
2
H
Y
0

V
0

y
+
k
3
2
X
0

V
0
2
x
-α
k
6
Z
0
zv-
k
f
v
,

y
=α
k
6
Z
0
V
0
zv
k
1
H
X
0
x+
k
2
A
2
H
+
k
f

Y
0
,
where
τ=t/
T
0
,
x=X/
X
0
,
z=Z/
Z
0
, and
v=V/
V
0
and the significance of all parameters (
k
i
for
i=1,…,7
,
A
,
H
,
C
,
α
,
β
,
τ
,
X
0
,
Y
0
, and
Z
0
) is given in [1].
Here, the bifurcation parameter is
k
f
, the inverse of the reactor's residence time.