The Discriminatory Power of Diagnostic Information from Discrete Medical Tests
The Discriminatory Power of Diagnostic Information from Discrete Medical Tests
A useful diagnostic test should provide information that helps to discriminate between competing hypotheses. But any practical diagnostic will be imperfect: both false positive and false negative indications are to be expected. So just how useful is a diagnostic test when it is, necessarily, imperfect? In [1], p. 44 shows a static, graphical example of how Bayes's theorem may be used to understand the factors determining the discriminatory power of diagnostic tests. This Demonstration is a dynamic version of that argument.
Let be the logical truth value (1 or 0) of a proposition about a state variable (e.g., a disease or health risk is present or absent), and let be the logical truth value (1 or 0) of a proposition about the outcome of an indicative imperfect diagnostic test (e.g., an X-ray or blood test measurement is either definitely positive or negative for this disease). From a statistical perspective there are three precise numerical inputs that feed into a coherent posterior inference about binary-valued after having observed the result of the binary-valued diagnostic signal : a sensitivity number, a specificity number, and a base rate number. The first two characterize uncertainty about the outcome of the diagnostic as a conditional probability under two different information conditions about the state . The sensitivity number expresses uncertainty about whether the diagnostic test will be positive, that is, , assuming that is true. The specificity number expresses an uncertainty about whether the diagnostic test for will be negative, that is, , assuming that is true. The third number, the base rate number, is a marginal or unconditional probability, , characterizing uncertainty about the binary state variable in the absence of, or prior to knowing, any diagnostic information .
S
D
S
D
D
S
P(D=1|S=1)
D
D=1
S=1
P(D=0|S=0)
D
S=1
D=0
S=0
P(S=1)
S
D
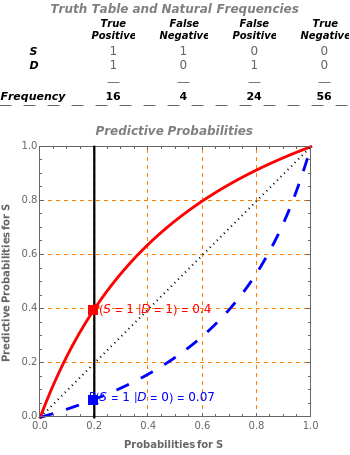
The discriminatory power of diagnostic information can be measured by the levels and differences between two inverse conditional probability assessments, and , one for each possible diagnostic test result. This interactive Demonstration creates a graphical depiction of the inverse probabilities and as functions of the underlying sensitivity, specificity, and base rate inputs. A natural frequency representation of the full joint probability distribution over the random variables (, ) is provided in a truth table format above the graph, where the column entries are frequency counts or "cases" in a hypothetical population of a fixed size.
P(S|D=1)
P(S|D=0)
P(S|D=1)
P(S|D=0)
S
D