The Convection-Diffusion Equation
The Convection-Diffusion Equation
Consider the unsteady-state convection-diffusion problem described by the equation:
∂c
∂t
2
∂
∂
2
x
∂c
∂x
where and are the diffusion coefficient and the velocity, respectively.
D
v
The initial and boundary conditions are:
t=0
c(x,0)=0
x=0
c(0,t)=1
x=∞
c(∞,t)=0
where is the concentration and is the position.
c
x
This problem has an analytical solution:
c(x,t)=erfc+erfc
1
2
x-vt
2
Dt
(vx)/D
e
x-+vt
2
Dt
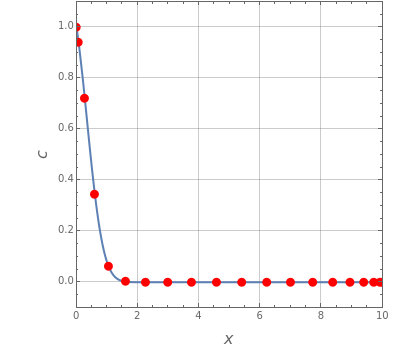
This Demonstration plots the solution . The numerical solution obtained using Chebyshev orthogonal collocation is given by the red dots. The analytical solution is given by the blue curve. Excellent agreement between the two solutions is observed. You can vary the values of , , and as well as the number of Chebyshev collocation points, .
c(x,t)
t
D
v
N+1