The Ballot Problem
The Ballot Problem
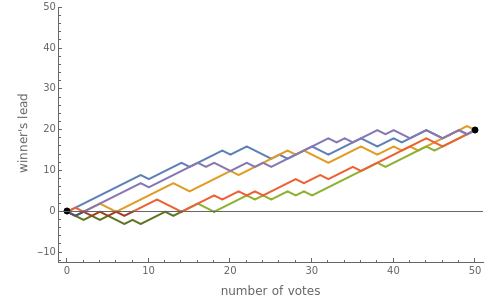
Consider an election with two candidates A and B resulting in votes for A and votes for B. If candidate A wins the election, the ballot problem is concerned with the probability that A was in the lead throughout the entire voting process. The ballot-counting process may be interpreted as a simple one-dimensional random walk with a step of for each vote for A and for each vote for B. The ballot problem asks for the probability that a simple random walk from to is strictly positive except at the origin. This probability turns out to be .
a
b
+1
-1
(0,0)
(a+b,a-b)
(a-b)/(a+b)
Choose "paths" to see the sample random walks representing an election with a specified winning margin . The portions of the paths below the horizontal axis are colored in a darker tone and represent the times during the vote-counting process when the winner was not in the lead.
a-b
Choose "histogram" to see a histogram of the fraction of times that the winner was in the lead, and the theoretical and observed probabilities that the winner was in the lead all the time. The empirical values are based on simulations of 1000 random walks as described above.