The Area of a Triangle, its Circumradius, and the Perimeter of its Orthic Triangle

A'B'

≈

3.80

B'C'

≈

3.97

A'C'

≈

2.05

p

≈

9.82

α

≈

19.85

R

≈

4.04

p

×

R

≈

39.69

2

α

≈

39.69

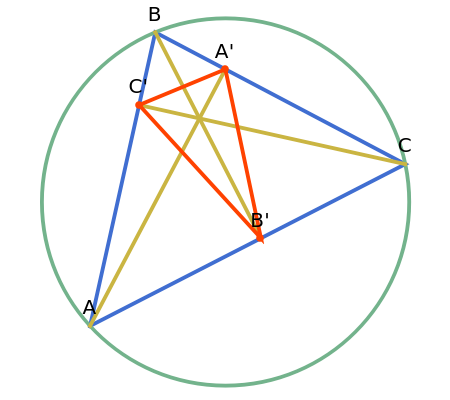
Let ABC be an acute triangle and A'B'C' be its orthic triangle (the triangle formed by the endpoints of the altitudes of ABC). Let

p

be the perimeter of A'B'C',

R

be the circumradius of ABC, and

α

be the area of ABC. Then

p×R=2α

.