WOLFRAM NOTEBOOK

WOLFRAM|DEMONSTRATIONS PROJECT

Static Longitudinal Stability of Fixed Wing Aircraft

center of gravity location

side-slip angle

stabilize

without feedback

with angle of attack feedback

elevator deflection

•	saturated control
•	unsaturated control

For an aircraft to achieve static longitudinal stability, its pitching moment must be perfectly balanced. The pitching moment coefficient,

, for a fixed-wing aircraft depends on several factors, notably, the angle of attack, center of gravity location, and the elevator deflection. In addition to being balanced, stability is an important consideration. For stability, the pitch stiffness of the aircraft given by the stability derivative

∂

∂α

(where

is the angle of attack) must be negative. This ensures a restoring moment if the aircraft is disturbed from its equilibrium position due to disturbances like wind gusts. Discussions on static longitudinal stability can be found in several texts (for example, Etkin and Reid 1996).

In this Demonstration the static longitudinal stability of an F-16 aircraft is explored. The model (Morelli 1998) is valid in the range:

-0.17450≤ α≤ 0.7854

-0.5236≤β≤0.5236

, and

-0.4363≤

≤0.4363

. Again

is the angle of attack,

is the side-slip angle, and

is the elevator deflection. All the angles are in radians and

denotes the center of gravity (c.g.) location.

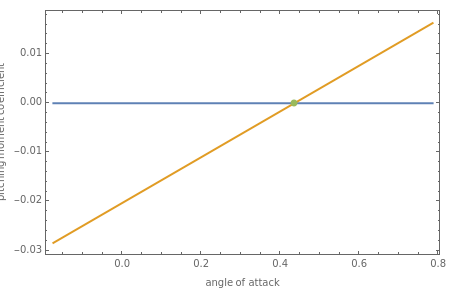
The F-16 is an inherently unstable aircraft. With the c.g. at the reference location of 0.35 and in straight flight (

β=0

), the aircraft has an unstable equilibrium at

α=0.4353

. It is not possible to stabilize it with any elevator deflection. With feedback of the angle of attack a feedback law

can be implemented. For example, at straight and level flight for

κ=0.35

=-0.7+1.8α

gives a stable trim condition at

α=0.386

. The green point signifies that there is sufficient elevator control with this condition. A red point denotes equilibrium points that are saturated. With this feedback law there are two other equilibrium points

α=-0.1374

and

α=0.6925

, at which the elevator is saturated and the aircraft is unstable as well. This gives a sense of the flight envelope in which the proportional feedback law is feasible. Similarly, various other configurations can be explored.

You are using a browser not supported by the Wolfram Cloud

Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.

I understand and wish to continue anyway »