Stability of a Linear Two-Dimensional Autonomous System

.

x

=

a

1

x +

b

1

y

a

1

1

b

1

1

.

y

=

a

2

x +

b

2

y

a

2

2

b

2

2

stability character

Consider the two-dimensional linear autonomous system



x

=

a

1

x+

b

1

y



y

=

a

2

x+

b

2

y

and define the matrix

M=

a 1	b 1
a 2	b 2

.

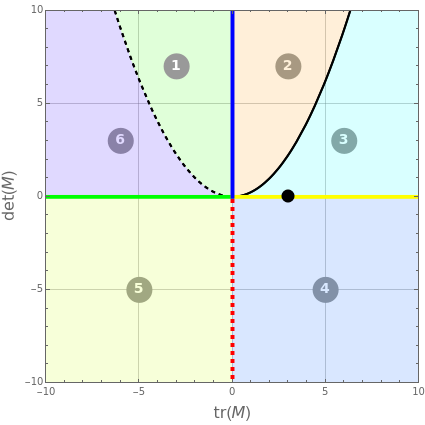
This Demonstration plots the phase portrait and the vector field of directions around the critical point

(0,0)

. This steady-state is indicated by the green dot in the phase plane diagram. In addition, the eigenvalues of

M

, the trace

tr(M)

, the determinant

M

, and

Δ=

2

tr

(M)-4M

are computed.

A plot of the curve obeying the equation

Δ=0

is obtained if you select the stability character tab. This parabola is indicated in solid and dashed black curves for positive and negative values of

tr(M)

, respectively.

The stability character of the steady-state is obtained by looking at the position of the black dot relative to the different colored regions (numbered 1–6).

region	eigenvalues	origin	tr(M)	M	Δ

1	complexconjugateswithnegativerealpart	asymptoticallystable	-	+	-
2	complexconjugateswithpositiverealpart	unstablespiral	+	+	-
3	realandpositive	unstableimpropernode	+	+	+
4,5	realwithoppositesigns	saddlepoint		-	+
6	realandnegative	asymptoticallystableimpropernode	-	+	+

green,-xaxis	……	marginallystable	-		+
yellow,+xaxis	……	unstable	+	0	+
blue,+yaxis	pureimaginary	centerwithalimitcycle	0	+	-
solidblackcurve	real,positive,andequal	unstablenodes	+	+	0
dashedblackcurve	real,negative,andequal	stablenodes	-	+	0