Squeeze Theorem

n

0

1

2

3

zoom

Let

f

,

g

, and

h

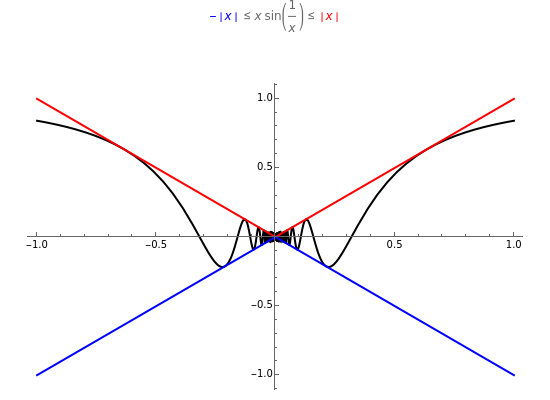
be functions satisfying

f(x)≤g(x)≤h(x)

for all

x

near

a

, except possibly at

a

. By the squeeze theorem, if

lim

xa

f(x)=

lim

xa

h(x)=L

then

lim

xa

g(x)=L

. Hence,

lim

x0

n

x

sin

1

x

equals zero if

n=1,2

, or

3

, since

n

x

sin

1

x

is squeezed between

-|

n

x

|

and

|

n

x

|

. The theorem does not apply if

n=0

, since

sin

1

x

is trapped but not squeezed. For

n=0

the limit does not exist, because no matter how close

x

gets to zero, there are values of

x

near zero for which

sin

1

x

=1

and some for which

sin

1

x

=-1

.