Soliton Trajectories for the Kadomtsev-Petviashvili Equation
Soliton Trajectories for the Kadomtsev-Petviashvili Equation
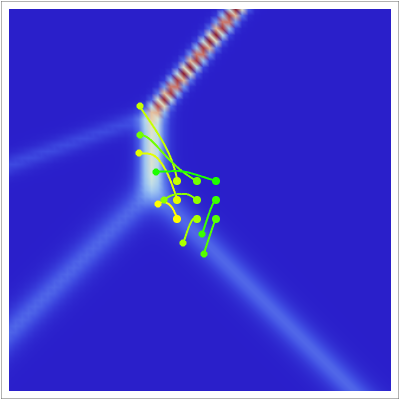
This Demonstration shows a particle-based fluid trajectory description of multi-soliton interactions. The Kadomtsev-Petviashvili (KP) equation is the two-dimensional version (2+1 dimensions, including time) of the Korteweg–de Vries (KdV) equation and supports multi-soliton-solutions. These solutions produce a pattern of straight lines in the plane at time . In particular, the KP equation describes approximately the slow evolution of waves in shallow water of uniform depth. Solitons are stable waves in space and time, in which the velocity depends on the amplitude. When solitons interact with other solitons, their shapes do not change, but their phase shifts. The trajectory method for quantum motion, developed by Louis de Broglie and David Bohm, is applied to the KP equation. In this method the motion of idealized particles is governed by the current flow, which is derived directly from the continuity equation; is proportional to the density of the wave in which idealized particles are positioned at the point at time . The current flow divided by the density establishes the guiding equation (velocity field) for the individual path of the particles in the wave. With , it yields the starting points of possible trajectories inside the wave, which lead to single trajectories governed by the velocity of the wave. Only the dynamic of the wave influences the motion of the particles. The trajectories are the streamlines of the wave, regarded as paths of idealized particles, because the particles themselves do not interact and do not influence the wave. Here the trajectories show the particle transfer of the wave in the fluid medium. The graphic shows the wave density, the trajectories, and the initial and actual position of idealized particles in the wave.
N
x
-y
t
u(x,y,t)
(x,y)
t
u(,,t=0)=
x
0
y
0
x 0 |
y 0 |