Simultaneous Heat and Moisture Transfer in a Porous Cylinder

time plot



0.0005

time

600.

ℒ

0.005

radius r/L

0.5

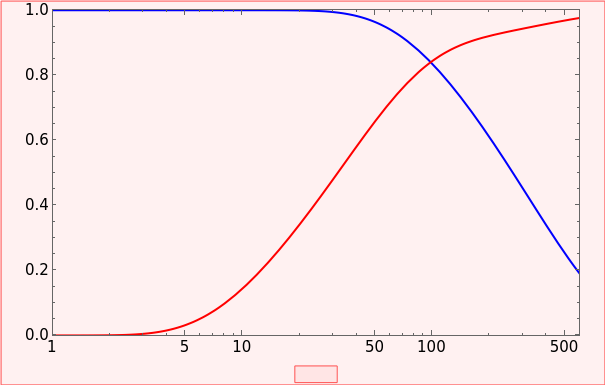
This Demonstration illustrates a model of heat and moisture transfer accompanied by phase change in a porous cylinder. The porous cylinder is initially at a constant temperature and moisture. It is suddenly placed in contact with a stream of hot air that exchanges heat and moisture by diffusion and convection. The moisture movement and the phase change occurring within the cylinder generate a coupled relationship between mass and heat transfer.

The governing equations [1] for this model are the Luikov equations:

∂T

∂t

=ℒ

1

r

∂

∂r

r

∂T

∂r

+

∂U

∂t

,

∂U

∂t

=

1

r

∂

∂r

r

∂U

∂r

+

1

r

∂

∂r

r

∂T

∂r

.

Here

T

and

U

are temperature and moisture potential, respectively,

r

is the space coordinate,

t

is time,



and



are positive coupling coefficients determined by moisture and heat migration, respectively, and

ℒ

and



represent the temperature and moisture diffusion coefficients.