Similar Triangles Determined by Miquel Circles and the Circumcircle

A

1

B

1

C

1

B

2

A

2

C

2

≈

30.89°

A

2

B

2

C

2

≈

88.74°

A

2

C

2

B

2

≈

60.37°

B

3

A

3

C

3

≈

30.89°

A

3

B

3

C

3

≈

88.74°

A

3

C

3

B

3

≈

60.37°

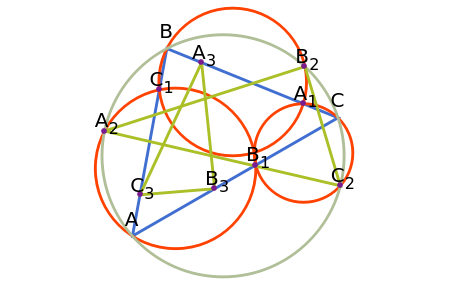
Let ABC be a triangle and let

A

1

,

B

1

, and

C

1

be points on BC, CA, and AB, respectively. Suppose that the circumcircles of

AB

1

C

1

,

BC

1

A

1

, and

CA

1

B

1

(the Miquel circles) intersect the circumcircle of ABC at points

A

2

,

B

2

, and

C

2

, respectively, where

A

2

≠A

,

B

2

≠B

, and

C

2

≠C

. Let

A

3

,

B

3

, and

C

3

be symmetric to

A

1

,

B

1

, and

C

1

with respect to the midpoints of BC, CA, and AB, respectively. Then

A

2

B

2

C

2

and

A

3

B

3

C

3

are similar.