Seader's Method for Real Roots of a Nonlinear Equation

function

Seader

Bessel J

plot

root list

u

1

0.99999

n

1

Consider the two test functions:

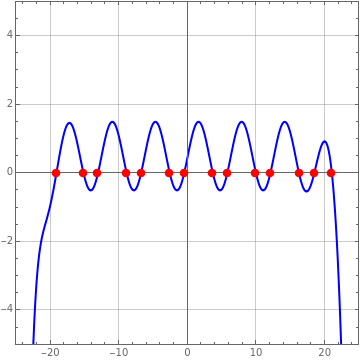
1. Seader's function:

f(x)=sin(x)-

cosh(x)

5000

z

1

+0.5

, where

z

1

=

u

1

1-

u

1

,

2. Bessel function of the first kind:

f(x)=

J

n

(x)

where

n

is an integer.

Seader's function admits multiple real roots (up to 14 roots for

u

1

=0.99999

) while Bessel's function has an infinite number of roots.

This Demonstration finds all the roots using Seader's approach [1] and the arc length continuation technique.

The problem considered is described as follows:

H(t(s),x(s))=1-t(s)+f(x(s))=0

(the function

H(t,x)

was first proposed in [1]) and

t'

2

(s)

+x'

2

(s)

=1

(i.e., the auxiliary equation). Using the built-in Mathematica function WhenEvent, all roots of

f(x)

are readily obtained when

t(s)=1

. A list of all roots is provided for both test functions. When you compare the present approach for the Bessel function of the first kind with the built-in Mathematica function BesselJZero perfect agreement is found.